题目内容
17. 二次函数 y=x2+bx+c的图象经过点(1,0),(3,0).
二次函数 y=x2+bx+c的图象经过点(1,0),(3,0).(1)求b、c的值;
(2)求出该二次函数图象的顶点坐标和对称轴方程;
(3)在所给坐标系中画出二次函数y=x2+bx+c的图象,并根据图象直接写出不等式x2+bx+c>0的解集.
分析 (1)将点(1,0)、(3,0)代入y=x2+bx+c,得到关于b、c的方程组,解方程组即可得b、c的值;
(2)根据(1)中b、c的值可得函数解析式,将其配方成顶点式可得顶点坐标及对称轴;
(3)由抛物线开口方向、与坐标轴的交点及顶点坐标可画出函数图象,根据图象即可得不等式的解集.
解答 解:(1)将(1,0),(3,0)代入 y=x2+bx+c,
得:$\left\{\begin{array}{l}{1+b+c=0}\\{9+3b+c=0}\end{array}\right.$,
解得:b=-4,c=3;
(2)由(1)知抛物线解析式为:y=x2-4x+3=(x-2)2-1,
顶点坐标为(2,-1),对称轴为直线x=2;
(3)函数图象如下: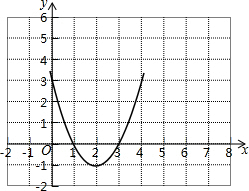
由图象可知,不等式x2+bx+c>0的解集为x<1或x>3.
点评 主要考查了二次函数的图象的性质以及二次函数和一元二次方程、一元二次不等式的关系,要会根据图象求顶点坐标和方程的解,解题时,一定要数形结合.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
5.下列方程是一元二次方程的是( )
| A. | 2x+y=0 | B. | x-4=5x | C. | x2-3x=6 | D. | x+$\frac{4}{x}$=1 |
12.下列说法中,正确的是( )
| A. | 若两个有理数的差是正数,则这两个数都是正数 | |
| B. | 两数相乘,积一定大于每一个乘数 | |
| C. | 0减去任何有理数,都等于此数的相反数 | |
| D. | 倒数等于本身的为1,0,-1 |
9. 某区八年级有3000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计
某区八年级有3000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计
(1)补全不完整的统计图表;
(2)样本中成绩的中位数落在哪一组;
(3)若将得分转化为等级,规定:50≤x<60评为D,60≤x<70评为C,70≤x<90评为B,90≤x<100评为A.这次全区八年级参加竞赛的学生约有多少学生参赛成绩被评为“B”?
 某区八年级有3000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计
某区八年级有3000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计| 成绩x(分) | 频数 | 频率 |
| 50≤x<60 | 10 | a |
| 60≤x<70 | 16 | 0.08 |
| 70≤x<80 | b | 0.20 |
(2)样本中成绩的中位数落在哪一组;
(3)若将得分转化为等级,规定:50≤x<60评为D,60≤x<70评为C,70≤x<90评为B,90≤x<100评为A.这次全区八年级参加竞赛的学生约有多少学生参赛成绩被评为“B”?
6.下列判断中唯一正确的是( )
| A. | 函数y=ax2的图象开口向上,函数y=-ax2的图象开口向下 | |
| B. | 二次函数y=ax2,当x<0时,y随x的增大而增大 | |
| C. | y=2x2与y=-2x2图象的顶点、对称轴、开口方向、开口大小完全相同 | |
| D. | 抛物线y=ax2与y=-ax2的图象关于x轴对称 |
 如图,已知点B的坐标为(10,0),点P(t,0)是OB上的一个动点,在x轴上方作等边△OPE和△BPF,连接EF,G为EF的中点.
如图,已知点B的坐标为(10,0),点P(t,0)是OB上的一个动点,在x轴上方作等边△OPE和△BPF,连接EF,G为EF的中点.