题目内容
20.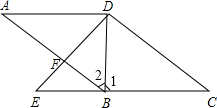 已知,如图,在四边形ABCD中,AD∥BC,点E在CB的延长线上,连接DE,交AB于点F,连接DB,且∠AFD=∠DBE,∠DBE=∠CDE.
已知,如图,在四边形ABCD中,AD∥BC,点E在CB的延长线上,连接DE,交AB于点F,连接DB,且∠AFD=∠DBE,∠DBE=∠CDE.(1)求证:四边形ABCD是平行四边形;
(2)当BD平分∠ABC时,求证:四边形ABCD是菱形.
分析 (1)欲证明四边形ABCD是平行四边形,结合已知条件,只需推知AB∥DC即可;
(2)有(1)可知:∠DBE=∠CDE,利用角平分线的性质和平行线的判定以及平行四边形的判定方法证明四边形ABCD为平行四边形,再证明AB=AD即可证明:四边形ABCD是菱形.
解答  (1)证明:∵∠AFD=∠DBE,∠DBE=∠CDE,
(1)证明:∵∠AFD=∠DBE,∠DBE=∠CDE,
∴∠AFD=∠CDE,
∴AB∥DC.
又∵AD∥BC,
∴四边形ABCD是平行四边形.
(2)证明:∵AD∥BC,
∴∠ADB=∠1.
又∵BD平分∠ABC,
∴∠1=∠2,
∴∠ADB=∠2,
∴AB=AD,而四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
点评 本题综合性的考查了平行线的判定和性质、平行四边形的判定及性质和菱形的判定方法,题目的综合性较强.

练习册系列答案
相关题目
12.A,B两地盛产桃,A地有桃400吨,B地有桃300吨.现将这些桃运到C、D两个冷藏仓库,已知C仓库可储存320吨,D仓库可储存380吨;从A地运往C、D两处的费用分别为每吨20元和25元,从B地运往C、D两处的费用分别为每吨15元和18元.设从A地运往C仓库的桃重量为x吨,A、B两地运往两仓库的桃运输费用分别为yA元和yB元.
(1)请填写下表后分别求出yA,yB与x之间的函数关系式,并写出定义域.
(2)试讨论A,B两地中,哪个运费较少?
(1)请填写下表后分别求出yA,yB与x之间的函数关系式,并写出定义域.
| 仓库 产地 | C | D | 总计 |
| A | x吨 | 400吨 | |
| B | 300吨 | ||
| 总计 | 320吨 | 380 | 700吨 |
 推理填空:
推理填空: