题目内容
5.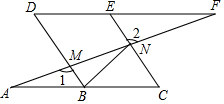 如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.
分析 (1)由已知角相等,利用对顶角相等,等量代换得到同位角相等,进而得出DB与EC平行,再由内错角相等两直线平行得到DE与BC平行,即可得证;
(2)由角平分线得到一对角相等,再由两直线平行内错角相等,等量代换得到一对角相等,再利用等角对等边得到CN=BC,再由平行四边形对边相等即可确定出所求.
解答 (1)证明:∵∠A=∠F,
∴DE∥BC,
∵∠1=∠2,且∠1=∠DMF,
∴∠DMF=∠2,
∴DB∥EC,
则四边形BCED为平行四边形;
(2)解:∵BN平分∠DBC,
∴∠DBN=∠CBN,
∵EC∥DB,
∴∠CNB=∠DBN,
∴∠CNB=∠CBN,
∴CN=BC=DE=2.
点评 此题考查了平行四边形的判定与性质,熟练掌握平行四边形的判定与性质是解本题的关键.

练习册系列答案
相关题目
20.a、b是实数,点A(2,a)、B(3,b)在反比例函数y=-$\frac{2}{x}$的图象上,则( )
| A. | a<b<0 | B. | b<a<0 | C. | a<0<b | D. | b<0<a |
7.在平面直角坐标系中,将抛物线y=x2-4先向右平移2个单位,再向上平移2个单位,得到的抛物线的表达式是( )
| A. | y=(x-2)2-2 | B. | y=(x+2)2+2 | C. | y=(x-2)2+2 | D. | y=(x+2)2-2 |
4.下列函数中,满足y的值随x的值增大而增大的是( )
| A. | y=3x-1 | B. | y=-2x | C. | y=$\frac{1}{x}$ | D. | y=x2 |
 如图,∠AOB=90°,OE是∠AOB的平分线,OD是∠BOC的平分线,若∠EOD=70°,则∠BOC的度数是50°.
如图,∠AOB=90°,OE是∠AOB的平分线,OD是∠BOC的平分线,若∠EOD=70°,则∠BOC的度数是50°.