题目内容
13.已知|x+y-5|+(x-y+3)2=0,则x=1,y=4.分析 根据已知等式,利用非负数的性质列出方程组,求出方程组的解即可得到x与y的值.
解答 解:∵|x+y-5|+(x-y+3)2=0,
∴$\left\{\begin{array}{l}{x+y=5①}\\{x-y=-3②}\end{array}\right.$,
①+②得:2x=2,即x=1,
把x=1代入①得:y=4,
故答案为:1;4
点评 此题考查了解二元一次方程组,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
3.如图,边长为2m+3的正方形纸片剪出一个边长为m+3的正方形之后,剩余部分可剪拼成一个长方形,若拼成的长方形一边长为m,则另一边长为( )
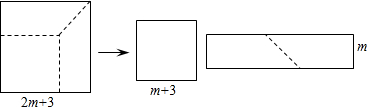

| A. | 2m+6 | B. | 3m+6 | C. | 2m2+9m+6 | D. | 2m2+9m+9 |
8.已知a,b,c为△ABC的三边长,关于x的一元二次方程(a+c)x2+2bx+(a-c)=0有两个相等的实数根,则△ABC为( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
18.某品牌电脑的成本为2400元,标价为4200元,如果商店要以利润率不低于5%的售价打折销售,最低可打( )折出售.
| A. | 6折 | B. | 7折 | C. | 7.5折 | D. | 8折 |
5.方程x2=x+1的解是( )
| A. | x=$\frac{1±\sqrt{5}}{2}$ | B. | x=$\sqrt{x+1}$ | C. | x=±$\sqrt{x+1}$ | D. | 无实数根 |
 如图,正方形ABCD和正方形CEFG中,点D在DG上,BC=1,CE=3,H是AF的中点,求CH的长.
如图,正方形ABCD和正方形CEFG中,点D在DG上,BC=1,CE=3,H是AF的中点,求CH的长.