题目内容
8.已知a,b,c为△ABC的三边长,关于x的一元二次方程(a+c)x2+2bx+(a-c)=0有两个相等的实数根,则△ABC为( )| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
分析 由跟的判别式△=(-2b)2-4(a+c)(a-c)=0,整理得出b2+c2=a2,由勾股定理逆定理得出△ABC的形状即可.
解答 解:∵关于x的一元二次方程(a+c)x2-2bx+a-c=0有两个相等的实数根,
∴△=(-2b)2-4(a+c)(a-c)=0,
整理得b2+c2=a2,
∴△ABC是以a为斜边的直角三角形.
故选C.
点评 本题考查了根的判别式,勾股定理的逆定理.一元二次方程根的情况与判别式△的关系:
(1)△>0,方程有两个不相等的实数根;
(2)△=0,方程有两个相等的实数根;
(3)△<0,方程没有实数根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.若a>b,则下列式子中一定成立的是( )
| A. | a-2<b-2 | B. | $\frac{a}{2}$>$\frac{b}{2}$ | C. | 2a>b | D. | 3-a>3-b |
16.若a>b,则下列各式变形正确的是( )
| A. | a-2<b-2 | B. | -2a<-2b | C. | |a|>|b| | D. | a2>b2 |
20.方程2x+3y=15的正整数解有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无数个 |
18.若点M(1-m,2+m)在第四象限,则m的取值范围是( )
| A. | m<1 | B. | m>-2 | C. | m<-2 | D. | -2<m<1 |
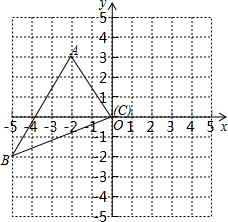 △ABC的位置如图所示:
△ABC的位置如图所示: