题目内容
3. 如图,已知F是DE的中点,∠D=∠E,∠DFN=∠EFM.求证:DM=EN.
如图,已知F是DE的中点,∠D=∠E,∠DFN=∠EFM.求证:DM=EN.
分析 证出∠DFM=∠EFN,由ASA证明△DFM≌△EFN,即可得出结论DM=EN.
解答 证明:∵点F是DE的中点,
∴DF=EF,
∵∠DFN=∠EFM,
∴180°-∠DFN=180°-∠EFM,
∴∠DFM=∠EFN,
在△DFM和△EFN中,$\left\{\begin{array}{l}{∠D=∠E}&{\;}\\{DF=EF}&{\;}\\{∠DFM=∠EFN}&{\;}\end{array}\right.$,
∴△DFM≌△EFN(ASA)
∴DM=EN.
点评 本题考查了全等三角形的判定与性质、邻补角定义;证明三角形全等是解决问题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
14.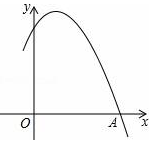 如图是二次函数y=ax2+bx+c图象的一部分,其图象的对称轴是直线x=1,且过点A(3,0),则下列结论正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其图象的对称轴是直线x=1,且过点A(3,0),则下列结论正确的是( )
 如图是二次函数y=ax2+bx+c图象的一部分,其图象的对称轴是直线x=1,且过点A(3,0),则下列结论正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其图象的对称轴是直线x=1,且过点A(3,0),则下列结论正确的是( )| A. | ac>0 | B. | 4a+2b+c<0 | C. | a-b+c>0 | D. | b2>4ac |
15.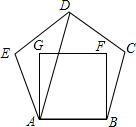 如图,把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG的度数是( )
如图,把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG的度数是( )
 如图,把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG的度数是( )
如图,把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG的度数是( )| A. | 30 | B. | 28 | C. | 20 | D. | 18 |
13.甲队修路1000m与乙队修路800m所用天数相同,已知甲队比乙队每天多修20m,设甲队每天修路x m.依题意,下面所列方程正确的是( )
| A. | $\frac{1000}{x}$=$\frac{800}{x-20}$ | B. | $\frac{1000}{x}$=$\frac{800}{x+20}$ | C. | $\frac{1000}{x-20}$=$\frac{800}{x}$ | D. | $\frac{1000}{x+20}$=$\frac{800}{x}$ |

 如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域.为了测量受污染的圆形区域的直径,在对应⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30°,∠ACD=60°,则直径AD=150$\sqrt{3}$米.
如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域.为了测量受污染的圆形区域的直径,在对应⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30°,∠ACD=60°,则直径AD=150$\sqrt{3}$米.