题目内容
20. 如图,△ABC
如图,△ABC(1)尺规作图:读下列语句,作出有关图形,保留作图痕迹.
①作∠ABC的角平分线,交AC于点D;
②作线段BD的垂直平分线,分别交AB,BC于点E,F,垂足为O;
③连接ED,FD.
(2)根据(1)中条件和图形,求证:ED=FD.
分析 (1)根据角平分线和中垂线的基本作图可得;
(2)由DE=BE、BF=DF、∠BOE=∠BOF=90°且∠EBO=∠FBO,证△EBO≌△FBO得BE=BF,即可得DE=DF.
解答 解:(1)如图所示;
(2)∵EF是BD的垂直平分线,
∴DE=BE、BF=DF,∠BOE=∠BOF=90°,
∵BD是∠ABC的平分线,
∴∠EBO=∠FBO,
在△EBO和△FBO中,
∵$\left\{\begin{array}{l}{∠EOB=∠FOB}\\{BO=BO}\\{∠EBO=∠FBO}\end{array}\right.$,
∴△EBO≌△FBO(ASA),
∴BE=BF,
∴DE=DF.
点评 本题主要考查角平分线和中垂线的基本作图及全等三角形的判定与性质,熟练掌握中垂线的性质和角平分线的定义得出全等三角形是解题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
15.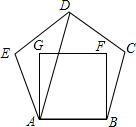 如图,把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG的度数是( )
如图,把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG的度数是( )
 如图,把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG的度数是( )
如图,把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG的度数是( )| A. | 30 | B. | 28 | C. | 20 | D. | 18 |
9.已知α为锐角,tanα=$\sqrt{3}$,则cosα等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
 如图:小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB与AD,使他们分别落在角的两边上,过点A、C画一条射线AE,AE就是∠PRQ的平分线.试利用全等知识,说明角平分仪的画图原理.
如图:小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB与AD,使他们分别落在角的两边上,过点A、C画一条射线AE,AE就是∠PRQ的平分线.试利用全等知识,说明角平分仪的画图原理. 如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域.为了测量受污染的圆形区域的直径,在对应⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30°,∠ACD=60°,则直径AD=150$\sqrt{3}$米.
如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域.为了测量受污染的圆形区域的直径,在对应⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30°,∠ACD=60°,则直径AD=150$\sqrt{3}$米.