题目内容
11.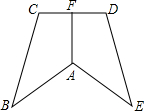 已知:如图,AB=AE,∠B=∠E,BC=ED,AF⊥CD,求证:CF=DF.
已知:如图,AB=AE,∠B=∠E,BC=ED,AF⊥CD,求证:CF=DF.
分析 连接AC,AD,证明三角形全等,得到等腰三角形,由三线合一得到结论.
解答  证明:连接AC,AD,
证明:连接AC,AD,
在△ABC与△AED中,$\left\{\begin{array}{l}{AB=AE}\\{∠B=∠E}\\{BC=ED}\end{array}\right.$
∴△ABC≌△AED,
∴AC=AD,
∵AF⊥CD,
∴CF=DF.
点评 本题考查了全等三角形的判定与性质,等腰三角形的性质,作辅助线是解题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
19.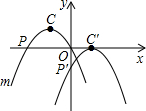 如图,已知在平面直角坐标系xOy中,抛物线m:y=-2x2-2x的顶点为C,与x轴两个交点为P,Q.现将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在y轴上,则下列各点的坐标不正确的是( )
如图,已知在平面直角坐标系xOy中,抛物线m:y=-2x2-2x的顶点为C,与x轴两个交点为P,Q.现将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在y轴上,则下列各点的坐标不正确的是( )
 如图,已知在平面直角坐标系xOy中,抛物线m:y=-2x2-2x的顶点为C,与x轴两个交点为P,Q.现将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在y轴上,则下列各点的坐标不正确的是( )
如图,已知在平面直角坐标系xOy中,抛物线m:y=-2x2-2x的顶点为C,与x轴两个交点为P,Q.现将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在y轴上,则下列各点的坐标不正确的是( )| A. | C(-$\frac{1}{2}$,$\frac{1}{2}$) | B. | C′(1,0) | C. | P(-1,0) | D. | P′(0,-$\frac{1}{2}$) |
6. 如图所示是某几何体的三视图,则该几何体的侧面积是( )
如图所示是某几何体的三视图,则该几何体的侧面积是( )
 如图所示是某几何体的三视图,则该几何体的侧面积是( )
如图所示是某几何体的三视图,则该几何体的侧面积是( )| A. | $\sqrt{10}$π | B. | 2$\sqrt{10}$π | C. | 3π | D. | 6π |
16.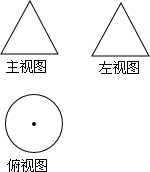 一个几何体的三视图如图所示,其中主视图与左视图都是边长为2的等边三角形,则这个几何体的侧面积为( )
一个几何体的三视图如图所示,其中主视图与左视图都是边长为2的等边三角形,则这个几何体的侧面积为( )
 一个几何体的三视图如图所示,其中主视图与左视图都是边长为2的等边三角形,则这个几何体的侧面积为( )
一个几何体的三视图如图所示,其中主视图与左视图都是边长为2的等边三角形,则这个几何体的侧面积为( )| A. | 4π | B. | 3π | C. | 2π | D. | $\sqrt{3}$π |
3.关于m的不等式-m>1的解为( )
| A. | m>0 | B. | m<0 | C. | m<-1 | D. | m>-1 |
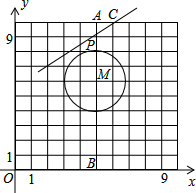 如图,点M的坐标为(5,6),⊙M的半径为2,点A,B,C都在网格的格点上,现有一点P在线段AB上运动.
如图,点M的坐标为(5,6),⊙M的半径为2,点A,B,C都在网格的格点上,现有一点P在线段AB上运动.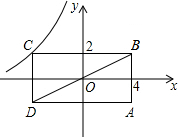 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=$\frac{k}{x}$的图象上,若点A的坐标为(4,-2),则k的值为-8.
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=$\frac{k}{x}$的图象上,若点A的坐标为(4,-2),则k的值为-8.