题目内容
1.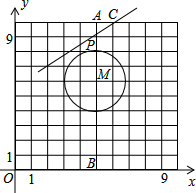 如图,点M的坐标为(5,6),⊙M的半径为2,点A,B,C都在网格的格点上,现有一点P在线段AB上运动.
如图,点M的坐标为(5,6),⊙M的半径为2,点A,B,C都在网格的格点上,现有一点P在线段AB上运动.(1)当点P在⊙M上时,请直接写出点P的坐标;
(2)点C的坐标为(7,10),作射线CP与⊙M相交时,求此时点P的纵坐标y的取值范围.
分析 (1)因为P、M都在直线AB上,且点M的坐标为(5,6),⊙M的半径为2,结合图象即可求得P的坐标;
(2)过C点作⊙M的切线,交⊙M于D、E,求得切线CE平行于AB,CD=CE=4,连接MD,作PF⊥CE于F,则四边形EFPM是矩形,PD⊥CD,然后证得△PMD≌△CPF,得出PD=CF,设PD=CF=x,则CP=4-x,根据勾股定理得出(4-x)2=22+x2,解得x=$\frac{3}{2}$,从而求得P的坐标,进而求得点P的纵坐标y的取值范围.
解答  解:(1)∵P、M都在直线AB上,且点M的坐标为(5,6),⊙M的半径为2,
解:(1)∵P、M都在直线AB上,且点M的坐标为(5,6),⊙M的半径为2,
∴当点P在⊙M上时,点P的坐标为(5,8)或(5,4);
(2)如图,过C点作⊙M的切线,交⊙M于D、E,
∵点C的坐标为(7,10),点M的坐标为(5,6),⊙M的半径为2,
∴切线CE平行于AB,与AB没有交点,
CD=CE=4,
连接MD,作PF⊥CE于F,则四边形EFPM是矩形,PD⊥CD,
∴PF=ME=MD=2,∠MPF=90°,
∴∠DPM=∠PCF,
在△PMD和△CPF中,
$\left\{\begin{array}{l}{∠DPM=∠PCF}\\{∠PDM=∠CFP=90°}\\{DM=PF}\end{array}\right.$,
∴△PMD≌△CPF(AAS),
∴PD=CF,
设PD=CF=x,则CP=4-x,
在RT△PCF中,(4-x)2=22+x2,
解得,x=$\frac{3}{2}$,
∴p的纵坐标为10-$\frac{3}{2}$=$\frac{17}{2}$,
∴射线CP与⊙M相交时,点P的纵坐标y的取值范围是0≤y≤$\frac{17}{2}$.
点评 本题考查了切线的判定和性质,坐标和图形性质,直线和圆的位置关系,三角形全等的判定和性质,熟练掌握性质定理是解题的关键.

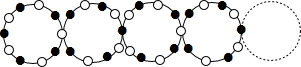
(1)把下列表格补充完整
| 圆环串中圆环的个数 | 1 | 2 | 3 | 4 | 5 | … |
| 实心圆圈和空心圆圈的总个数 | 10 | 19 | 28 | 37 | 46 | … |
(3)如果圆环串由这样的圆环20个组成,那么需要多少个空心圆圈?
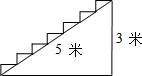 如图所示,在高为3m,斜坡长为5m的楼梯表面铺地毯,至少需要地毯7米.
如图所示,在高为3m,斜坡长为5m的楼梯表面铺地毯,至少需要地毯7米.
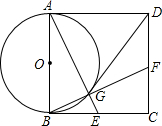 如图,在正方形ABCD中,G是以AB为直径的圆上一点,连接AG并延长交BC于点E,连接BG并延长交CD于点F.
如图,在正方形ABCD中,G是以AB为直径的圆上一点,连接AG并延长交BC于点E,连接BG并延长交CD于点F.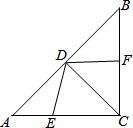 如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD是∠ACB的角平分线,点E、F分别是边AC、BC上的动点.AB=$\sqrt{32}$,设AE=x,BF=y.
如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD是∠ACB的角平分线,点E、F分别是边AC、BC上的动点.AB=$\sqrt{32}$,设AE=x,BF=y.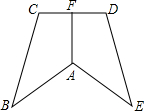 已知:如图,AB=AE,∠B=∠E,BC=ED,AF⊥CD,求证:CF=DF.
已知:如图,AB=AE,∠B=∠E,BC=ED,AF⊥CD,求证:CF=DF.