题目内容
19.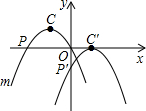 如图,已知在平面直角坐标系xOy中,抛物线m:y=-2x2-2x的顶点为C,与x轴两个交点为P,Q.现将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在y轴上,则下列各点的坐标不正确的是( )
如图,已知在平面直角坐标系xOy中,抛物线m:y=-2x2-2x的顶点为C,与x轴两个交点为P,Q.现将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在y轴上,则下列各点的坐标不正确的是( )| A. | C(-$\frac{1}{2}$,$\frac{1}{2}$) | B. | C′(1,0) | C. | P(-1,0) | D. | P′(0,-$\frac{1}{2}$) |
分析 根据抛物线m的解析式求得点P、C的坐标,然后由点P′在y轴上,点C′在x轴上得到平移规律,由此可以确定点P′、C′的坐标.
解答 解:∵y=-2x2-2x=-2x(x+1)或y=-2(x+$\frac{1}{2}$)2+$\frac{1}{2}$,
∴P(-1,0),O(0,0),C(-$\frac{1}{2}$,$\frac{1}{2}$).
又∵将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在y轴上,
∴该抛物线向下平移了$\frac{1}{2}$个单位,向右平移了1个单位,
∴C′($\frac{1}{2}$,0),P′(0,-$\frac{1}{2}$).
综上所述,选项B符合题意.
故选:B.
点评 主要考查了函数图象的平移,抛物线与坐标轴的交点坐标的求法,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.会利用方程求抛物线与坐标轴的交点.

练习册系列答案
相关题目
4.下面说法正确的是( )
| A. | ${(\frac{π}{2})}^{0}$是无理数 | B. | $\frac{\sqrt{3}}{2}$是有理数 | C. | $\frac{7}{5}$是无理数 | D. | $\root{3}{-27}$是有理数 |
8.△ABC的一边长为5,另两边分别是方程x2-6x+m=0的两根,则m的取值范围是( )
| A. | m>$\frac{11}{4}$ | B. | $\frac{11}{4}$<m≤9 | C. | $\frac{11}{4}$≤m≤9 | D. | m≤$\frac{11}{4}$ |
 如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD是∠ACB的角平分线,点E、F分别是边AC、BC上的动点.AB=$\sqrt{32}$,设AE=x,BF=y.
如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD是∠ACB的角平分线,点E、F分别是边AC、BC上的动点.AB=$\sqrt{32}$,设AE=x,BF=y.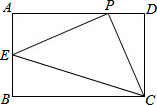 已知在矩形ABCD中,AB=2,BC=3,P是AD边上任意一点,(不含端点A、D),连接PC,过点P作PE⊥PC交AB于点E,在点P运动过程中,连接EC,是否存在∠ECP=∠DCP的情况?若存在,求出此时BE的长;若不存在,请说明理由.
已知在矩形ABCD中,AB=2,BC=3,P是AD边上任意一点,(不含端点A、D),连接PC,过点P作PE⊥PC交AB于点E,在点P运动过程中,连接EC,是否存在∠ECP=∠DCP的情况?若存在,求出此时BE的长;若不存在,请说明理由.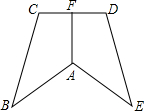 已知:如图,AB=AE,∠B=∠E,BC=ED,AF⊥CD,求证:CF=DF.
已知:如图,AB=AE,∠B=∠E,BC=ED,AF⊥CD,求证:CF=DF.