题目内容
6.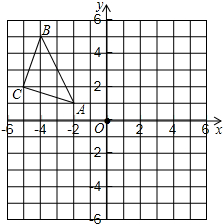 如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).
如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).(1)作△ABC关于直线l:x=-1对称的△A1B1C1,并写出点A、B、C的对称点A1、B1、C1的坐标;
(2)将△A1B1C1绕点O顺时针旋转90°,画出图形,并求出A1B1旋转过程中划过的面积.
分析 (1)根据轴对称的性质得出对应点的位置,画出图形,写出点A、B、C的对称点A1、B1、C1的坐标即可;
(2)根据图形旋转性质得出对应点的位置,即可画出图形,根据勾股定理求出OA1、OB1的长度,S扇形OB1B2-S扇形OA1A2即为所求.
解答 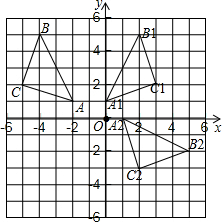 解:(1)如图所示,△A1B1C1即为所求,A1(0,1),B1(2,5),C1(3,2);
解:(1)如图所示,△A1B1C1即为所求,A1(0,1),B1(2,5),C1(3,2);
(2)如图所示,△A2B2C2即为所求,
∵OA1=1,OB1=$\sqrt{29}$,∠A1OA2=∠B1OB2=90°
∴A1B1旋转过程中划过的面积=S扇形OB1B2-S扇形OA1A2=$\frac{90π×(\sqrt{29})^{2}}{360}$-$\frac{90π×{1}^{2}}{360}$=7π.
点评 本题考查了轴对称和图形的旋转以及扇形面积的求法,求出对应点的位置是解决问题的关键.

练习册系列答案
相关题目
 的解是正数,则a的取值范围是_________.
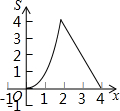
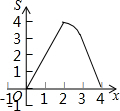
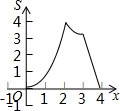
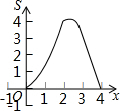
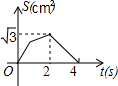
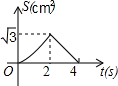
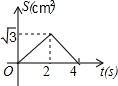
的解是正数,则a的取值范围是_________.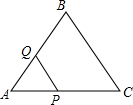 如图,在等边△ABC的边长为2cm,点P从点A出发,以1cm/s的速度向点C移动,同时点Q从点A出发,以1cm/s的速度沿AB-BC的方向向点C移动,若△APQ的面积为S(cm2),则下列最能反映S(cm2)与移动时间t(s)之间函数关系的大致图象是( )
如图,在等边△ABC的边长为2cm,点P从点A出发,以1cm/s的速度向点C移动,同时点Q从点A出发,以1cm/s的速度沿AB-BC的方向向点C移动,若△APQ的面积为S(cm2),则下列最能反映S(cm2)与移动时间t(s)之间函数关系的大致图象是( )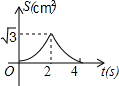
 如图,在矩形ABCD中,AB=4,AD=2,点P、Q同时从点A出发,点P以每秒2个单位的速度沿A→B→C→D的方向运动;点Q以每秒1个单位的速度沿A→D→C的方向运动,当P、Q两点相遇时,它们同时停止运动.设P、Q两点运动的时间为x(秒),△APQ的面积为S(平方单位),则△APQ的面积S与运动时间x之间的函数图象大大致形状是( )
如图,在矩形ABCD中,AB=4,AD=2,点P、Q同时从点A出发,点P以每秒2个单位的速度沿A→B→C→D的方向运动;点Q以每秒1个单位的速度沿A→D→C的方向运动,当P、Q两点相遇时,它们同时停止运动.设P、Q两点运动的时间为x(秒),△APQ的面积为S(平方单位),则△APQ的面积S与运动时间x之间的函数图象大大致形状是( )