题目内容
15．
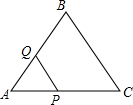如图，在等边△ABC的边长为2cm，点P从点A出发，以1cm/s的速度向点C移动，同时点Q从点A出发，以1cm/s的速度沿AB-BC的方向向点C移动，若△APQ的面积为S（cm2），则下列最能反映S（cm2）与移动时间t（s）之间函数关系的大致图象是（ ）| A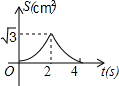． |  | B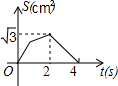． |  | C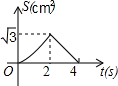． |  | D． |  |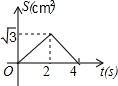
分析 当0≤t≤2和2＜t≤4时，分别求出函数解析式，根据函数的性质分析即可得出结论．
解答 解：当0≤t≤2时，S=$\frac{1}{2}•t•sin{60°}t=\frac{{\sqrt{3}}}{4}{t^2}$，
此函数抛物线开口向上，且函数图象为抛物线右侧的一部分；
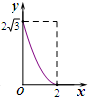
当2＜t≤4时，S=$\frac{1}{2}×2•sin{60°}（4-t）=-\frac{{\sqrt{3}}}{2}t+2\sqrt{3}$，
此函数图象是直线的一部分，且S随t的增大而减小．
所以符合题意的函数图象只有C．
故选：C．
点评 本题主要考查了动点问题的函数图形，分段讨论，求出函数表达式是解决问题的关键．
练习册系列答案
相关题目
某运动员在图所示的场地上匀速跑步，他从点A出发，沿箭头所示方向经过点B跑到点C，共用时30秒．他的教练选择了一个固定的位置Q观察他的跑步过程．设跑步的时间为t（单位：秒），他与教练的距离为y（单位：米）．下列能反映y与t的函数关系的大致图象是（ ）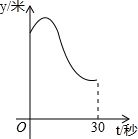
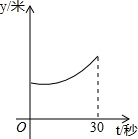
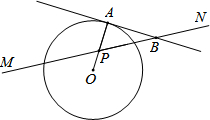如图，⊙O的半径为2，点P是半径OA上的一个动点，过点P作直线MN且∠APN=60°，过点A的切线AB交MN于点B．设OP=x，△PAB的面积为 y，则下列图象中，能表示y与x的函数关系的图象大致是（ ）
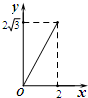
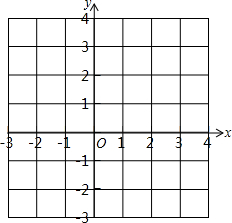如图，已知O是坐标原点，A、B两点的坐标分别为（3，-1）、（2，1）．
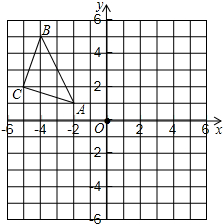如图，△ABC在平面直角坐标系中，其中，点A、B、C的坐标分别为A（-2，1），B（-4，5），C（-5，2）．
选做题：从甲乙两题中选作一题，如果两题都做，只以甲题计分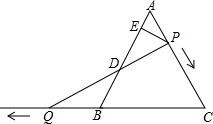
如图，已知△ABC是等腰三角形，且∠C=60°，AB=10，点P是AC边上一动点，由点A向点C运动（点P与点A、C不重合），Q是CB延长线上一点，与 点P同时以相同的速度由点B向CB延长线方向运动（点Q与点B不重合），过点P作PE⊥AB于点E，连结PQ交AB于点D．