题目内容
10. 如图,在矩形ABCD中,AB=4,AD=2,点P、Q同时从点A出发,点P以每秒2个单位的速度沿A→B→C→D的方向运动;点Q以每秒1个单位的速度沿A→D→C的方向运动,当P、Q两点相遇时,它们同时停止运动.设P、Q两点运动的时间为x(秒),△APQ的面积为S(平方单位),则△APQ的面积S与运动时间x之间的函数图象大大致形状是( )
如图,在矩形ABCD中,AB=4,AD=2,点P、Q同时从点A出发,点P以每秒2个单位的速度沿A→B→C→D的方向运动;点Q以每秒1个单位的速度沿A→D→C的方向运动,当P、Q两点相遇时,它们同时停止运动.设P、Q两点运动的时间为x(秒),△APQ的面积为S(平方单位),则△APQ的面积S与运动时间x之间的函数图象大大致形状是( )| A. | 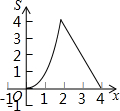 | B. | 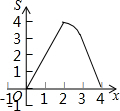 | C. | 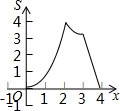 | D. | 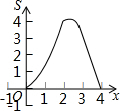 |
分析 当0≤x≤2时,P点在AB上,Q点在AD上,根据三角形面积进行计算即可;
当2<x≤3时,P点在CB上,PB=2x-4,CP=6-2x,Q点在CD上,DQ=x-2,QC=6-x,用长方形ABCD的面积-三角形ADQ的面积-三角形QCP的面积-三角形ABP的面积可得三角形QAP的面积;
当3<x≤4时,则QP=4-DQ-CP=12-3x,再利用三角形面积进行计算即可;
解答 解:如图1,
当0≤x≤2时,S=$\frac{1}{2}$AP=$\frac{1}{2}$•x•2x=x2.
如图2,
当2<x≤3时,
由长方形ABCD的面积-S△ADQ-S△QCP-S△ABP=S△QAP
=4×2-$\frac{1}{2}$×2×(x-2)-$\frac{1}{2}$×4×(2x-4)-$\frac{1}{2}$×(6-x)×(6-2x)
=-x2+4x.
如图3,
当3<x≤4时,S=$\frac{1}{2}$×AD×QP=$\frac{1}{2}$×2×(12-3x)=12-3x.
故选:D.
点评 此题主要考查了动点问题的函数图象,关键是根据x的取值范围表示出S与x之间的函数关系式.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
19.为了了解一批产品的质量,从中抽取300个产品进行检验,在这个问题中,被抽取的300个产品叫做( )
| A. | 总体 | B. | 个体 | C. | 总体的一个样本 | D. | 普查方式 |
 ______;
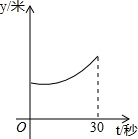
______; 某运动员在图所示的场地上匀速跑步,他从点A出发,沿箭头所示方向经过点B跑到点C,共用时30秒.他的教练选择了一个固定的位置Q观察他的跑步过程.设跑步的时间为t(单位:秒),他与教练的距离为y(单位:米).下列能反映y与t的函数关系的大致图象是( )
某运动员在图所示的场地上匀速跑步,他从点A出发,沿箭头所示方向经过点B跑到点C,共用时30秒.他的教练选择了一个固定的位置Q观察他的跑步过程.设跑步的时间为t(单位:秒),他与教练的距离为y(单位:米).下列能反映y与t的函数关系的大致图象是( )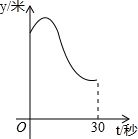


 如图,已知O是坐标原点,A、B两点的坐标分别为(3,-1)、(2,1).
如图,已知O是坐标原点,A、B两点的坐标分别为(3,-1)、(2,1).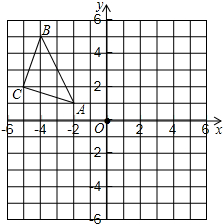 如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).
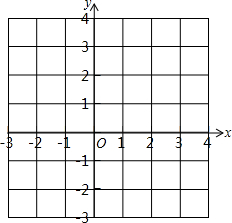
如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).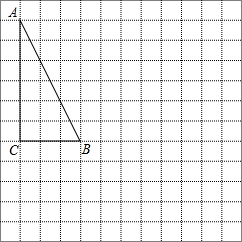 在下面的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,BC=3,AC=6.
在下面的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,BC=3,AC=6.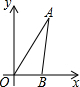 选做题:从甲乙两题中选作一题,如果两题都做,只以甲题计分
选做题:从甲乙两题中选作一题,如果两题都做,只以甲题计分