题目内容
4.先化简,再求值:($\frac{2}{x-2}-\frac{1}{x}$)$÷\frac{{x}^{2}-4}{{x}^{2}-2{x}^{2}}$,其中x=-$\frac{2}{3}$.分析 先把括号内通分和除法运算化为乘法运算,再把分子分母因式分解后约分得到原式=$\frac{x}{x-2}$,然后把x的值代入计算即可.
解答 解:原式=$\frac{2x-(x-2)}{x(x-2)}$•$\frac{{x}^{2}(x-2)}{(x+2)(x-2)}$
=$\frac{x+2}{x(x-2)}$•$\frac{{x}^{2}(x-2)}{(x+2)(x-2)}$
=$\frac{x}{x-2}$,
当x=-$\frac{2}{3}$时,原式=$\frac{-\frac{2}{3}}{-\frac{2}{3}-2}$=$\frac{1}{4}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
12.计算$\frac{4}{{a}^{2}-2a}-\frac{a}{a-2}$的结果是( )
| A. | $\frac{a+2}{a}$ | B. | $-\frac{a+2}{a}$ | C. | $\frac{a-2}{a}$ | D. | -$\frac{a-2}{a}$ |
9.在△ABC中,∠C=90°,tanA=$\frac{3}{4}$,那么sinA的值为( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{3}$ |
2.我国许多银行的商标设计中都融入了中国古代钱币的图案,下图是我国四大银行的商标图案,其中可以看做是轴对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
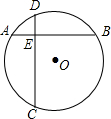 如图,⊙O中弦AB⊥CD于E,AE=2,EB=6,ED=3,则⊙O的半径为$\frac{\sqrt{65}}{2}$.
如图,⊙O中弦AB⊥CD于E,AE=2,EB=6,ED=3,则⊙O的半径为$\frac{\sqrt{65}}{2}$. 如图,四边形ABCD中,连接AC,AB∥DC,要使AD=BC,需要添加的一个条件是AB=CD(答案不唯一).
如图,四边形ABCD中,连接AC,AB∥DC,要使AD=BC,需要添加的一个条件是AB=CD(答案不唯一).