题目内容
12.计算$\frac{4}{{a}^{2}-2a}-\frac{a}{a-2}$的结果是( )| A. | $\frac{a+2}{a}$ | B. | $-\frac{a+2}{a}$ | C. | $\frac{a-2}{a}$ | D. | -$\frac{a-2}{a}$ |
分析 首先将原式进行通分运算,进而因式分解化简求出答案.
解答 解:$\frac{4}{{a}^{2}-2a}-\frac{a}{a-2}$
=$\frac{4}{a(a-2)}$-$\frac{{a}^{2}}{a(a-2)}$
=$\frac{4-{a}^{2}}{a(a-2)}$
=$\frac{(2-a)(2+a)}{a(a-2)}$
=-$\frac{2+a}{a}$.
故选:B.
点评 此题主要考查了分式的加减运算,正确进行因式分解是解题关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
3.下列整式的运算中,结果正确的是( )
| A. | 3+x=3x | B. | y+y+y=y3 | C. | 6ab-ab=6 | D. | 3a3b-3ba3=0 |
20.在0,$\sqrt{3}$,2,-3这四个数中,最大的数是( )
| A. | 0 | B. | $\sqrt{3}$ | C. | 2 | D. | -3 |
7.若$\frac{y}{x}=\frac{1}{4}$,则$\frac{x+2y}{x}$的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{2}{3}$ |
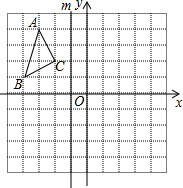 如图所示的正方形网格中,每个小正方形的边长为1,△ABC的三个顶点都在格点上.
如图所示的正方形网格中,每个小正方形的边长为1,△ABC的三个顶点都在格点上. 如图,抛物线y=ax2+bx+c与y轴相交于点(0,$\frac{5}{2}$),与直线AB交于点A(-1,0),B(4,$\frac{5}{2}$),点D是抛物线A、B两点间部分上的一动点(不与点A、B重合),直线CD∥y轴,交直线AB于C,连接AD、BD.
如图,抛物线y=ax2+bx+c与y轴相交于点(0,$\frac{5}{2}$),与直线AB交于点A(-1,0),B(4,$\frac{5}{2}$),点D是抛物线A、B两点间部分上的一动点(不与点A、B重合),直线CD∥y轴,交直线AB于C,连接AD、BD.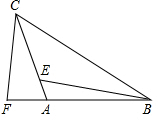 如图,在△ABC中,AB=CA,∠CAB=90°,F为BA延长线上一点,点E在线段AC上,
如图,在△ABC中,AB=CA,∠CAB=90°,F为BA延长线上一点,点E在线段AC上,