题目内容
关于x的分式方程
=1,下列说法正确的是( )
| m |
| x-3 |
| A、方程的解是x=m+3 |
| B、当m>-3时,方程的解是正数 |
| C、当m<-3时,方程的解是负数 |
| D、以上说法都不对 |
考点:分式方程的解
专题:
分析:先按照一般步骤解方程,用含有m的代数式表示x,然后根据x的取值讨论a的范围,即可作出判断.
解答:解:方程两边都乘以x-3,去分母得:m=x-3,
解得:x=m+3,
当x-3≠0,把x=m+3代入得:m+3-3≠0,即m≠0,方程有解,故选项A错误;
当x>0,即m+3>0,解得:m>-3,则当m>-3时,方程的解为正数,故选项B正确;
当x<0,即m+3<0,解得:m<-3,则m<-3且m≠0时,方程的解为负数,故选项C错误;
显然选项D错误.
故选:B.
解得:x=m+3,
当x-3≠0,把x=m+3代入得:m+3-3≠0,即m≠0,方程有解,故选项A错误;
当x>0,即m+3>0,解得:m>-3,则当m>-3时,方程的解为正数,故选项B正确;
当x<0,即m+3<0,解得:m<-3,则m<-3且m≠0时,方程的解为负数,故选项C错误;
显然选项D错误.
故选:B.
点评:考查了分式方程的解,解题关键是要掌握方程的解的定义,使方程成立的未知数的值叫做方程的解.本题在判断方程的解是负数时,容易忽视a≠0的条件.

练习册系列答案
相关题目
下列说法中不正确的是( )
| A、“某射击运动员射击一次,正中把靶心”属于随机事件 |
| B、“13名同学至少有两名同学的出生月份相同”属于必然事件 |
| C、“在标准大气压下,当温度降到-1℃时,水结成冰”属于随机事件 |
| D、“某袋中只有5个球,且都是黄球,任意摸出一球是白球”属于不可能事件 |
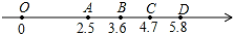 如图,数轴上有O、A、B、C、D五点,根据图中各点所表示的数,判断3
如图,数轴上有O、A、B、C、D五点,根据图中各点所表示的数,判断3| 2 |
| A、在线段OA上 |
| B、在线段AB上 |
| C、在线段BC上 |
| D、在线段CD上 |
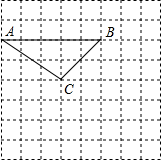 已知△ABC如图所示地摆放在边长为1的小正方形组成的网格内,将△ABC绕点C顺时针旋转90°,得到△A1B1C.
已知△ABC如图所示地摆放在边长为1的小正方形组成的网格内,将△ABC绕点C顺时针旋转90°,得到△A1B1C.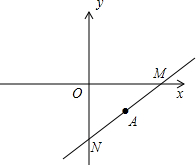 如图,已知A为直角三角形的外心,且坐标为(
如图,已知A为直角三角形的外心,且坐标为( 如图,AB=AC=9cm,BC=4cm,点A和点B关于直线l对称,AC与直线l相交于点D,则△BDC的周长是
如图,AB=AC=9cm,BC=4cm,点A和点B关于直线l对称,AC与直线l相交于点D,则△BDC的周长是