题目内容
在长为48cm的线段AB上,取一点D,使AD=
AB,C为AB的中点,则CD= cm.
| 1 |
| 3 |
考点:两点间的距离
专题:
分析:根据线段间的比例,可得AD的长,根据线段中点的性质,可得AC的长,根据线段的和差,可得答案.
解答:解:由AB=48(cm),AD=
AB,得
AD=
AB=
×48=16(cm).
由C为AB的中点,得
AC=
AB=
×48=24(cm),
由线段的和差,得
CD=AC-AD=24-16=8(cm),
故答案为:8.
| 1 |
| 3 |
AD=
| 1 |
| 3 |
| 1 |
| 3 |
由C为AB的中点,得
AC=
| 1 |
| 2 |
| 1 |
| 2 |
由线段的和差,得
CD=AC-AD=24-16=8(cm),
故答案为:8.
点评:本题考查了两个点间的距离,利用线段中点的性质得出AC的长,利用线段的和差.

练习册系列答案
相关题目
关于x的分式方程
=1,下列说法正确的是( )
| m |
| x-3 |
| A、方程的解是x=m+3 |
| B、当m>-3时,方程的解是正数 |
| C、当m<-3时,方程的解是负数 |
| D、以上说法都不对 |
在圆内接正十边形中,AB是正十边形的一条边,圆的半径为2,则圆内接正十边形的边长AB为( )
A、3-
| ||||
B、
| ||||
C、
| ||||
D、
|
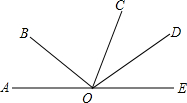 如图,点A、O、E在同一条直线上,∠AOB=40°,∠DOB=105°,OD平分∠COE.
如图,点A、O、E在同一条直线上,∠AOB=40°,∠DOB=105°,OD平分∠COE.