题目内容
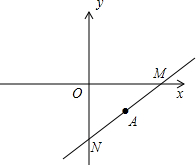 如图,已知A为直角三角形的外心,且坐标为(
如图,已知A为直角三角形的外心,且坐标为(| 3 |
| 2 |
考点:三角形的外接圆与外心,一次函数图象上点的坐标特征
专题:计算题
分析:设M(a,0),N(0,b),根据三角形外心的定义得到AM=AN,即点A为MN的中点,则利用线段的中点坐标公式
=
,
=-2,然后计算出a和b的值后即可得到M、N的坐标.
| a+0 |
| 2 |
| 3 |
| 2 |
| 0+b |
| 2 |
解答:解:设M(a,0),N(0,b),
∵A为直角三角形OMN的外心,
∴AM=AN,即点A为MN的中点,
∴
=
,
=-2,
解得a=3,b=-4,
∴M(3,0),N(0,-4).
∵A为直角三角形OMN的外心,
∴AM=AN,即点A为MN的中点,
∴
| a+0 |
| 2 |
| 3 |
| 2 |
| 0+b |
| 2 |
解得a=3,b=-4,
∴M(3,0),N(0,-4).
点评:本题考查了三角形的外接圆与外心:经过三角形的三个顶点的圆,叫做三角形的外接圆.三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.也考查了线段的中点坐标公式.

练习册系列答案
相关题目
关于x的分式方程
=1,下列说法正确的是( )
| m |
| x-3 |
| A、方程的解是x=m+3 |
| B、当m>-3时,方程的解是正数 |
| C、当m<-3时,方程的解是负数 |
| D、以上说法都不对 |
在圆内接正十边形中,AB是正十边形的一条边,圆的半径为2,则圆内接正十边形的边长AB为( )
A、3-
| ||||
B、
| ||||
C、
| ||||
D、
|
现已知线段a,b(a<b),∠MON=90°,求作Rt△ABO,使得∠O=90°,AB=b,小惠和小雷的作法分别如下.
小惠:①以点O为圆心、线段a为半径画弧,交射线ON于点A;②以点A为圆心、线段b长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
小雷:①以点O为圆心、线段a为半径画弧,交射线ON于点A;②以点O为圆心、线段b长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
则下列说法中正确的是( )
小惠:①以点O为圆心、线段a为半径画弧,交射线ON于点A;②以点A为圆心、线段b长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
小雷:①以点O为圆心、线段a为半径画弧,交射线ON于点A;②以点O为圆心、线段b长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
则下列说法中正确的是( )
| A、小惠的作法正确,小雷的作法错误 |
| B、小雷的作法正确,小惠的作法错误 |
| C、两人的作法都正确 |
| D、两人的作法都错误 |

 已知∠AOB=30°,点P在OA上,且OP=2,点P关于直线OB的对称点是Q,则PQ=
已知∠AOB=30°,点P在OA上,且OP=2,点P关于直线OB的对称点是Q,则PQ=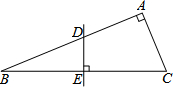 已知:在纸片上画有一直角三角形ABC,∠A=90°,∠B=22.5°,将其折叠,使点B与点C重合,折痕交AB于点D,交BC于点E,再将其打开,如图所示.若BD=3,求AB的长.
已知:在纸片上画有一直角三角形ABC,∠A=90°,∠B=22.5°,将其折叠,使点B与点C重合,折痕交AB于点D,交BC于点E,再将其打开,如图所示.若BD=3,求AB的长.