题目内容
14. 如图,在正方形ABCD中,E是AB上一点,BE=4,AE=3BE,P是AC上一动点,则PB+PE的最小值是( )
如图,在正方形ABCD中,E是AB上一点,BE=4,AE=3BE,P是AC上一动点,则PB+PE的最小值是( )| A. | 12+8$\sqrt{2}$ | B. | 20 | C. | 12+4$\sqrt{10}$ | D. | 16$\sqrt{2}$ |
分析 由正方形性质的得出B、D关于AC对称,根据两点之间线段最短可知,连接DE,交AC于P,连接BP,则此时PB+PE的值最小,进而利用勾股定理求出即可.
解答  解:如图,连接DE,交AC于P,连接BP,则此时PB+PE的值最小.
解:如图,连接DE,交AC于P,连接BP,则此时PB+PE的值最小.
∵四边形ABCD是正方形,
∴B、D关于AC对称,
∴PB=PD,
∴PB+PE=PD+PE=DE.
∵BE=4,AE=3BE,
∴AE=12,AB=16,
∴DE=$\sqrt{1{2}^{2}+1{6}^{2}}$=20,
故PB+PE的最小值是20.
故选B.
点评 本题考查了轴对称-最短路线问题,正方形的性质,解此题通常是利用两点之间,线段最短的性质得出.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
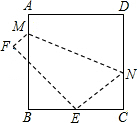 如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在点F处,折痕为MN,则$\frac{AM}{CN}$的值是$\frac{1}{3}$.
如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在点F处,折痕为MN,则$\frac{AM}{CN}$的值是$\frac{1}{3}$.
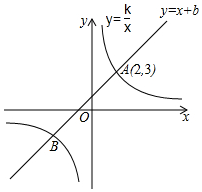 如图,已知一次函数y=x+b与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,其中点A的坐标为(2,3).
如图,已知一次函数y=x+b与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,其中点A的坐标为(2,3).
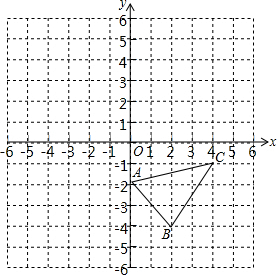 如图,平面直角坐标系中△ABC,分别画出与△ABC关于x轴、y轴对称的△A1B1C1和△A2B2C2,并写出△A1B1C1和△A2B2C2各顶点坐标.
如图,平面直角坐标系中△ABC,分别画出与△ABC关于x轴、y轴对称的△A1B1C1和△A2B2C2,并写出△A1B1C1和△A2B2C2各顶点坐标.