Question

4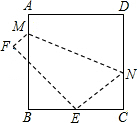．如图，将边长为8cm的正方形ABCD折叠，使点D落在BC边的中点E处，点A落在点F处，折痕为MN，则$\frac{AM}{CN}$的值是$\frac{1}{3}$．

Answer 1

分析 在Rt△ECN中，利用勾股定理与折叠性质，求出CN的长度；过点M作MG⊥CD于点C，证明△MNG≌△DEC，得到GN=CE，从而求出DG，即AM的长度，于是得到结论．

解答 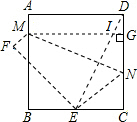解：设CN=xcm，则DN=（8-x）cm．
由折叠可知，EN=DN=（8-x）cm．
在Rt△ECN中，CE=4cm，CN=xcm，EN=（8-x）cm，
由勾股定理得：EN²=CN²+CE²，即（8-x）²=x²+4²，
解得：x=3，
∴CN=3cm；
如图，过点M作MG⊥CD于点G，则由题意可知AM=DG，MG=BC=CD．
连接DE，交MG于点I．
由折叠可知，DE⊥MN，∴∠NMG+MIE=90°，
∵∠DIG+∠EDC=90°，∠MIE=∠DIG（对顶角相等），
∴∠NMG=∠EDC．
在△MNG与△DEC中，$\left\{\begin{array}{l}{∠NMG=∠EDC}\\{MG=CD}\\{∠MGN=∠DCE=90°}\end{array}\right.$，
∴△MNG≌△DEC（ASA）．
∴GN=CE=4cm，
∴DG=CD-CN-GN=8-3-4=1cm．
∴AM=DG=1cm．
∴$\frac{AM}{CN}$的值是$\frac{1}{3}$，
故答案为：$\frac{1}{3}$．

点评 考查了翻折问题，翻折问题关键是找准对应重合的量，哪些边、角是相等的．本题中DN=EN是解题关键，再利用勾股定理、全等三角形的知识就迎刃而解．