题目内容
2.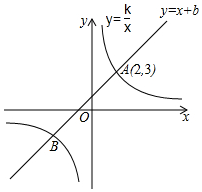 如图,已知一次函数y=x+b与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,其中点A的坐标为(2,3).
如图,已知一次函数y=x+b与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,其中点A的坐标为(2,3).(1)求点B的坐标;
(2)请根据图象直接写出不等式x+b>$\frac{k}{x}$的解集.
分析 (1)根据点A的坐标利用待定系数法,即可求出一次函数及反比例函数解析式,联立两函数解析式成方程组,解之即可得出点B的坐标;
(2)根据两函数图象的上下位置结合点A、B的横坐标,即可得出不等式的解集.
解答 解:(1)把点A的坐标(2,3)代入一次函数y=x+b中,
3=2+b,解得:b=1,
∴一次函数的解析式为y=x+1.
把点A的坐标(2,3)代入反比例函数y=$\frac{k}{x}$中,
3=$\frac{k}{2}$,解得:k=6,
∴反比例函数的解析式为y=$\frac{6}{x}$.
联立两函数解析式成方程组,
$\left\{\begin{array}{l}{y=x+1}\\{y=\frac{6}{x}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=3}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-3}\\{{y}_{2}=-2}\end{array}\right.$,
∴点B的坐标为(-3,-2).
(2)观察函数图象可知:当-3<x<0或x>2时,直线在双曲线的上方,
∴不等式x+1>$\frac{6}{x}$的解集为-3<x<0或x>2.
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求一次函数解析式以及待定系数法求反比例函数解析式,解题的关键是:(1)根据点A的坐标,利用待定系数法求出一次(反比例)函数解析式;(2)根据两函数图象的上下位置关系找出不等式的解集.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
14. 如图,在正方形ABCD中,E是AB上一点,BE=4,AE=3BE,P是AC上一动点,则PB+PE的最小值是( )
如图,在正方形ABCD中,E是AB上一点,BE=4,AE=3BE,P是AC上一动点,则PB+PE的最小值是( )
 如图,在正方形ABCD中,E是AB上一点,BE=4,AE=3BE,P是AC上一动点,则PB+PE的最小值是( )
如图,在正方形ABCD中,E是AB上一点,BE=4,AE=3BE,P是AC上一动点,则PB+PE的最小值是( )| A. | 12+8$\sqrt{2}$ | B. | 20 | C. | 12+4$\sqrt{10}$ | D. | 16$\sqrt{2}$ |
11.五边形共有( )条对角线.
| A. | 2 | B. | 4 | C. | 5 | D. | 6 |
 如图,抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,且BO=OC=3AO.
如图,抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,且BO=OC=3AO.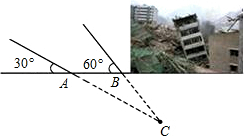 某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A,B相距3米,探测线与地面的夹角分别是30°和60°(如图),则生命所在点C距离地面的深度是2.6米.(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A,B相距3米,探测线与地面的夹角分别是30°和60°(如图),则生命所在点C距离地面的深度是2.6米.(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73) 两个有理数a、b在数轴上的位置如图所示,则a+b<0(填>,=,<).
两个有理数a、b在数轴上的位置如图所示,则a+b<0(填>,=,<).