题目内容
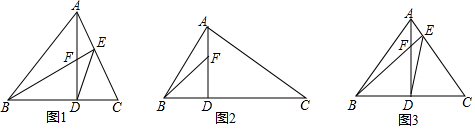
9.(1)如图1,锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE交于F,连DE,求证:DF•DA=DB•DC;(2)如图2,若∠BAC=90°,AD⊥BC于D,F为线段AD上一点,在AD延长线上找一点G使AD2=DF•DG,请画出图形找出点G并加以证明;
(3)如图3,在(1)的条件下,若∠ABC=45°,EF=1,EC=3,直接写出BD长.
分析 (1)只要证明△DBF∽△DAC即可解决问题;
(2)如图2中,在DC上截取DM,使得DM=DA,连接FM、AM,作MN⊥FM交AD的延长线于G.则AD2=DF•DG.只要证明△DMF∽△DGM即可解决问题;
(3)如图3中,连接FC.首先证明△BDF≌△ADC,推出DF=DC,想办法求出DF、DC,设BD=AD=y,则AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=$\sqrt{5+{y}^{2}}$,由△EAF∽△DAC,可得$\frac{AF}{AC}$=$\frac{EF}{DC}$,列出方程即可解决问题;
解答 (1)证明:如图1中,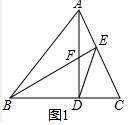
∵AD、AE是△ABC的高,
∴∠ADC=∠BDF=∠BEC=90°,
∴∠DBF+∠C=90°,∠DAC+∠C=90°,
∴∠DBF=∠DAC,
∴△DBF∽△DAC,
∴$\frac{BD}{AD}$=$\frac{DF}{DC}$,
∴DF•DA=DB•DC.
(2)解:如图2中,在DC上截取DM,使得DM=DA,
连接FM、AM,作MN⊥FM交AD的延长线于G.则AD2=DF•DG.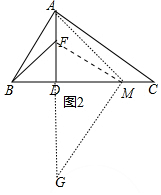
理由:∵∠MDF=∠MDG=∠FMG=90°,
∴∠DMF+∠DMG=90°,∠DMG+∠G=90°,
∴∠DMF=∠G,
∴△DMF∽△DGM,
∴$\frac{DM}{DG}$=$\frac{DF}{DM}$,
∴DM2=DF•DG,
∵AD=DM,
∴AD2=DF•DG.
(3)解:如图3中,连接FC.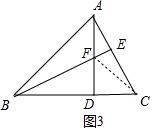
∵∠ABC=45°,∠ADB=90°,
∴BD=AD,
∵∠DBF=∠CAD(已证),∠BDF=∠ADC=90°,
∴△BDF≌△ADC,
∴DF=DC,
在Rt△EFC中,FC=$\sqrt{E{F}^{2}+E{C}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∴DF=DC=$\sqrt{5}$,设BD=AD=y,则AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=$\sqrt{5+{y}^{2}}$,
∵△EAF∽△DAC,
∴$\frac{AF}{AC}$=$\frac{EF}{DC}$,
∴$\frac{y-\sqrt{5}}{\sqrt{5+{y}^{2}}}$=$\frac{1}{\sqrt{5}}$,
解得y=2$\sqrt{5}$或$\frac{\sqrt{5}}{2}$(舍弃),
∴BD=2$\sqrt{5}$.
点评 本题考查相似形综合题、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理、等腰直角三角形的性质和判定等知识,解题的关键是正确寻找相似三角形解决问题,学会添加辅助线,构造相似三角形解决问题,属于中考压轴题.

| A. | $\sqrt{7}$ | B. | $\frac{11}{7}$ | C. | 4π | D. | $\root{3}{9}$ |
 如图,在正方形ABCD中,E是AB上一点,BE=4,AE=3BE,P是AC上一动点,则PB+PE的最小值是( )
如图,在正方形ABCD中,E是AB上一点,BE=4,AE=3BE,P是AC上一动点,则PB+PE的最小值是( )| A. | 12+8$\sqrt{2}$ | B. | 20 | C. | 12+4$\sqrt{10}$ | D. | 16$\sqrt{2}$ |
 图中有三个正方形,其中全等三角形有( )对.
图中有三个正方形,其中全等三角形有( )对.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
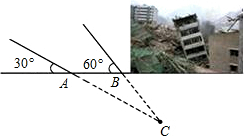 某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A,B相距3米,探测线与地面的夹角分别是30°和60°(如图),则生命所在点C距离地面的深度是2.6米.(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A,B相距3米,探测线与地面的夹角分别是30°和60°(如图),则生命所在点C距离地面的深度是2.6米.(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)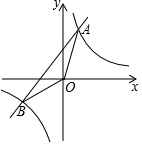 如图,一次函数y1=x+1的图象与反比例函数y2=$\frac{k}{x}$的图象交于A(m,2)、B两点.
如图,一次函数y1=x+1的图象与反比例函数y2=$\frac{k}{x}$的图象交于A(m,2)、B两点.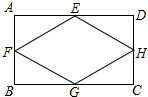 如图,E、F、G、H分别为矩形ABCD四边的中点.
如图,E、F、G、H分别为矩形ABCD四边的中点.