题目内容
有两条或两条以上对称轴的轴对称图形是（ ）
A. 等腰三角形 B. 角 C. 等边三角形 D. 锐角三角形
C
【解析】A.等腰三角形只有一条对称轴；
B.角也只有一条对称轴，是角平分线所在的直线；
C.等边三角形有三条对称轴；
D.锐角三角形的对称轴数量不确定.
故选：C
练习册系列答案
阅读快车系列答案
相关题目
在平面直角坐标系中，将点M（1，2）向左平移2个长度单位后得到点N，则点N的坐标是（ ）
A. （－1，2） B. （3，2） C. （1，4） D. （1，0）
A
【解析】根据坐标的平移变化的规律，左右平移只改变点的横坐标，左减右加。上下平移只改变点的纵坐标，下减上加。因此，
将点M（1，2）向左平移2个长度单位后得到点N的坐标是（1－2，2），即（－1，2）。故选A。 如图所示，根据图形把多项式a2+5ab+4b2因式分解=__．
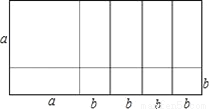
（a+b）（a+4b）
【解析】由图可知，
a2+5ab+4b2=（a+b）（a+4b）. 如图，P和Q为△ABC边AB与AC上两点，在BC边上求作一点M，使△PQM的周长最小．
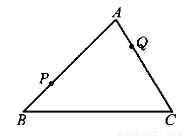
过P点作关于BC对称点P1 连接QP1 交BC于M点
【解析】 等腰三角形有一个是50°，它的一条腰上的高与底边的夹角是（ ）
A. 25° B. 40° C. 25°或40° D. 50°
C
【解析】∵等腰三角形有一个是50°
∴有两种可能
①是三个角为50°、50°、80°；②是三个角为50°、65°、65°分情况说明如下：
①当三个角为50°、50°、80°时，根据图①，可得其一条腰上的高与底边的夹角∠DAB=40°；
②当三个角为50°、65°、65°，根据图②，可得其一条腰上的高与底边的夹角∠DAB=25°故故选：C
① ② 下列图形中，不一定是轴对称图形的是（ ）
A. 等腰三角形 B. 等边三角形 C. 直角三角形 D. 等腰直角三角形
C
【解析】A.等腰三角形是轴对称图形，不符合题意；
B.等边三角形是轴对称图形，不符合题意；
C.直角三角形不一定是轴对称图形，符合题意；
D.等腰直角三角形是轴对称图形，不符合题意.
故选：C. 如图，在△ABC中，AB＝AC，AD⊥BC于D，E是AB上的一点，EF∥AD交CA的延长线于F.
求证：△AEF是等腰三角形．
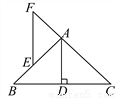
见解析
【解析】试题分析：首先根据等腰三角形底边上的三线合一定理可得：AD为∠BAC的角平分线，根据平行线的性质得出∠F=∠CAD，∠FEA=∠BAD，从而∠FEA=∠F，得出等腰三角形．
试题解析：∵AB=AC，AD⊥BC， ∴∠BAD=∠CAD， 又∵AD∥EF，
∴∠F=∠CAD，∠FEA=∠BAD， ∴∠FEA=∠F， ∴△AEF是等腰三角形． 如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度．他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°．已知A点的高度AB为2米，台阶AC的坡度为1：
（即AB：BC=1：），且B、C、E三点在同一条直线上．请根据以上条件求出树DE的高度（测倾器的高度忽略不计）．
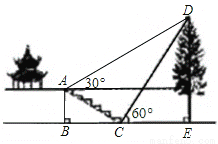
【解析】
因为直角三角形ABC中，BC=，AB=4， 所以BC=4，设DF=x，
在直角三角形AFD中，
,
在直角三角形DCE中，
,
所以
所以DE=米。
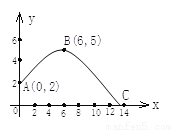
【解析】试题分析：由于AF⊥AB，则四边形ABEF为矩形，设DE=x，在Rt△CDE中，CE═==，在Rt△ABC中，得到，求出BC，在Rt△AFD中，求出AF，由AF=BC+CE即可求出x的长．... 在体育测试时，初三的一名高个子男生推铅球，已知铅球所经过的路线是某二次函数图象的一部分(如图)，若这个男生出手处A点的坐标为(0，2)，铅球路线的最高处B点的坐标为B(6，5).
(1)求这个二次函数的表达式；
(2)该男生把铅球推出去多远?(精确到0.01米).
（1）y= (x-6)2+5；（2）该男生把铅球推出约13.75米
【解析】试题分析：（1）根据顶点坐标B(6,5)可设函数关系式为y=a(x-6)2+5，再把A(0,2)代入即可求得结果；
（2）把y=0代入求得图象与x轴的交点坐标，即可得到结果.
(1)设y=a(x-6)2+5,
则由A(0,2)得2=a(0-6)2+5，解得a=.
故y= (x-6)2+5；
...