��Ŀ����
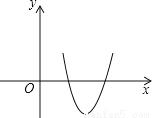
��ͼ�������κ���y=31x2-999x+892��ͼ�λ�������ƽ���ϣ��жϷ���31x2-999x+892=0����������������������ȷ��������
A. �������죬�Ҿ�Ϊ����
B. �������죬��ֻ��һ������
C. ������ͬ����Ϊ����
D. ������ͬ����Ϊ����
 A
���������߶��κ���y=31x2-999x+892��ͼ����x�����������㣬����x����������ཻ��
���31x2-999x+892=0��������ʵ����
��ѡ��A��
A
���������߶��κ���y=31x2-999x+892��ͼ����x�����������㣬����x����������ཻ��
���31x2-999x+892=0��������ʵ����
��ѡ��A��
����ͼ���м�����Գ�ͼ���������ĶԳ�ͼ�ε��ǣ� ��
A. �ȱ������� B. ���������� C. ���� D. ƽ���ı���
 C
������������������ȱ������β������ĶԳ�ͼ�Σ��Գ���Ϊ������������ֱ�ߣ����������β������ĶԳ�ͼ�Σ��Գ���Ϊ�ױ��ϵ���������ֱ�ߣ�ƽ���ı��εĶԳ�����Ϊ�����Խ��ߵĽ��㣬������Գ�ͼ�Σ����εĶԳ�����Ϊ�����Խ��ߵĽ��㣬�Գ���Ϊ�����Խ�������ֱ�ߣ�����ѡ��C��
C
������������������ȱ������β������ĶԳ�ͼ�Σ��Գ���Ϊ������������ֱ�ߣ����������β������ĶԳ�ͼ�Σ��Գ���Ϊ�ױ��ϵ���������ֱ�ߣ�ƽ���ı��εĶԳ�����Ϊ�����Խ��ߵĽ��㣬������Գ�ͼ�Σ����εĶԳ�����Ϊ�����Խ��ߵĽ��㣬�Գ���Ϊ�����Խ�������ֱ�ߣ�����ѡ��C�� ��ƽ��ֱ������ϵ�У�����M��1��2������ƽ��2�����ȵ�λ��õ���N�����N�������ǣ� ��
A. ����1��2�� B. ��3��2�� C. ��1��4�� D. ��1��0��
 A
�����������������ƽ�Ʊ仯�Ĺ��ɣ�����ƽ��ֻ�ı��ĺ����꣬����Ҽӡ�����ƽ��ֻ�ı��������꣬�¼��ϼӡ���ˣ�
����M��1��2������ƽ��2�����ȵ�λ��õ���N�������ǣ�1��2��2����������1��2������ѡA��
A
�����������������ƽ�Ʊ仯�Ĺ��ɣ�����ƽ��ֻ�ı��ĺ����꣬����Ҽӡ�����ƽ��ֻ�ı��������꣬�¼��ϼӡ���ˣ�
����M��1��2������ƽ��2�����ȵ�λ��õ���N�������ǣ�1��2��2����������1��2������ѡA�� ��֪һԪ���η���x2+px+q+1=0��һ��Ϊ2��
��1����q����p�Ĺ�ϵʽ��
��2����֤��������y=x2+px+q��x�����������㣻
 ��1��q= -2p-5����2��������
�������������������1����x=2��������q��p�Ĺ�ϵʽ��
��2���ɡ�=b2-4ac���ж���������x��Ľ������.
�����������1����x=2�����22+2p+q+1=0����q= -2p-5��
��2���ߡ�=p2-4q��0��
�ɣ�1���á�=p2+4��2p+5��=p2+8p+20=��p+4��2+4��0��
��һԪ���η���x2+px+...
��1��q= -2p-5����2��������
�������������������1����x=2��������q��p�Ĺ�ϵʽ��
��2���ɡ�=b2-4ac���ж���������x��Ľ������.
�����������1����x=2�����22+2p+q+1=0����q= -2p-5��
��2���ߡ�=p2-4q��0��
�ɣ�1���á�=p2+4��2p+5��=p2+8p+20=��p+4��2+4��0��
��һԪ���η���x2+px+... ��֪����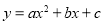 ��ͼ����ͼ��ʾ����ô����x�ķ���
��ͼ����ͼ��ʾ����ô����x�ķ��� �ĸ�������ǣ� ��
�ĸ�������ǣ� ��

A����ʵ����
B�����������ʵ����
C�����������ʵ��
D��������ͬ�Ų���ʵ����
 D��
��������
����������ߵ�ͼ����x�����������㣬����������������ǩ�3���߷��̣���ʱ������y=��2��x��ֵ����ͼ���֪��������ͬ�Ų���ʵ��������ѡD��
D��
��������
����������ߵ�ͼ����x�����������㣬����������������ǩ�3���߷��̣���ʱ������y=��2��x��ֵ����ͼ���֪��������ͬ�Ų���ʵ��������ѡD�� ������y=ax2+bx+c��a��0����x��Ľ����ǣ�-2��0���ͣ�4��0�������������ߵĶԳ����ǣ�������
A. ֱ��x=1 B. ֱ��x= -1 C. ֱ��x=2 D. ֱ��x= -2
 A
����������������y=ax2+bx+c��a��0����x��Ľ����ǣ�-2��0���ͣ�4��0����
�����������ߵĶԳ����ǣ�x=����x=1��
��ѡ��A��
A
����������������y=ax2+bx+c��a��0����x��Ľ����ǣ�-2��0���ͣ�4��0����
�����������ߵĶԳ����ǣ�x=����x=1��
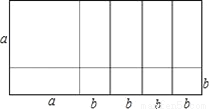
��ѡ��A�� ��ͼ��ʾ������ͼ�ΰѶ���ʽa2+5ab+4b2��ʽ�ֽ�=__��
 ��a+b����a+4b��
����������ͼ��֪��
a2+5ab+4b2=��a+b����a+4b��.
��a+b����a+4b��
����������ͼ��֪��
a2+5ab+4b2=��a+b����a+4b��. ��ͼ��P��QΪ��ABC��AB��AC�����㣬��BC��������һ��M��ʹ��PQM���ܳ���С��
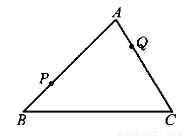
 ��P��������BC�ԳƵ�P1 ����QP1 ��BC��M��
��������
��P��������BC�ԳƵ�P1 ����QP1 ��BC��M��
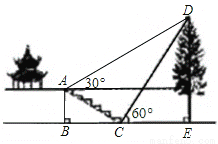
�������� ��ͼ��ijУ�ۺ�ʵ���С���ͬѧ����������һ����DE�ĸ߶ȣ��������������ǰ��һ��¥ͤǰ��̨����A�㴦���������D������Ϊ30�㣬����������ķ����ߵ�̨���µĵ�C�������������D������Ϊ60�㣮��֪A��ĸ߶�ABΪ2�ף�̨��AC���¶�Ϊ1�� ����AB��BC=1��
����AB��BC=1�� ������B��C��E������ͬһ��ֱ���ϣ�������������������DE�ĸ߶ȣ��������ĸ߶Ⱥ��Բ��ƣ���
������B��C��E������ͬһ��ֱ���ϣ�������������������DE�ĸ߶ȣ��������ĸ߶Ⱥ��Բ��ƣ���
 ��������
��Ϊֱ��������ABC�У�BC=��AB=4�� ����BC=4����DF=x��
��ֱ��������AFD�У�
,
��ֱ��������DCE�У�
,
����
����DE=�ס�
���������������������AF��AB�����ı���ABEFΪ���Σ���DE=x����Rt��CDE�У�CE�T==����Rt��ABC�У��õ������BC����Rt��AFD�У����AF����AF=BC+CE�������x�ij���...
��������
��Ϊֱ��������ABC�У�BC=��AB=4�� ����BC=4����DF=x��
��ֱ��������AFD�У�
,
��ֱ��������DCE�У�
,
����
����DE=�ס�
���������������������AF��AB�����ı���ABEFΪ���Σ���DE=x����Rt��CDE�У�CE�T==����Rt��ABC�У��õ������BC����Rt��AFD�У����AF����AF=BC+CE�������x�ij���... 
