题目内容
12.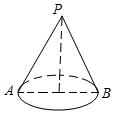 如图,这是某同学用纸板做成的一个底面直径为10cm,高为12cm的无底圆锥形玩具(接缝忽略不计),则做这个玩具所需纸板的面积是65πcm2(结果保留π).
如图,这是某同学用纸板做成的一个底面直径为10cm,高为12cm的无底圆锥形玩具(接缝忽略不计),则做这个玩具所需纸板的面积是65πcm2(结果保留π).
分析 作PO⊥AB于O.利用勾股定理求出PA,求出圆锥的表面积即可解决问题.
解答 解:作PO⊥AB于O.
在Rt△PAO中,PA=$\sqrt{O{P}^{2}+O{A}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13.
∴S表面积=π•5•13=65π.
∴做这个玩具所需纸板的面积是65πcm2.
故答案为65π.
点评 本题考查圆锥的表面积、解题的关键是记住圆锥的侧面积公式、底面积公式.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
20. 有这样一个问题:探究函数y=$\frac{1}{x}$+1的图象与性质.
有这样一个问题:探究函数y=$\frac{1}{x}$+1的图象与性质.
小明根据学习一次函数的经验,对函数y=$\frac{1}{x}$+1的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数y=$\frac{1}{x}$+1的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值.
求出m的值;
(3)如图,在平面直角坐标系xOy中,描出了以表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)写出该函数的一条性质该函数没有最大值或 该函数没有最小值.
 有这样一个问题:探究函数y=$\frac{1}{x}$+1的图象与性质.
有这样一个问题:探究函数y=$\frac{1}{x}$+1的图象与性质.小明根据学习一次函数的经验,对函数y=$\frac{1}{x}$+1的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数y=$\frac{1}{x}$+1的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值.
| x | … | -4 | -3 | -2 | -1 | -m | m | 1 | 2 | 3 | 4 | … |
| y | … | $\frac{3}{4}$ | $\frac{2}{3}$ | $\frac{1}{2}$ | 0 | -1 | 3 | 2 | $\frac{3}{2}$ | $\frac{4}{3}$ | $\frac{5}{4}$ | … |
(3)如图,在平面直角坐标系xOy中,描出了以表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)写出该函数的一条性质该函数没有最大值或 该函数没有最小值.
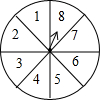 如图,转盘被平均分成8个区域,每个区域分别标注数字1、2、3、4、5、6、7、8,任意转动转盘一次,规定:如果指针恰好指在分割线上,那么重转一次,直到指针指向一个标有数字的区域为止.写出下列事件发生的概率:
如图,转盘被平均分成8个区域,每个区域分别标注数字1、2、3、4、5、6、7、8,任意转动转盘一次,规定:如果指针恰好指在分割线上,那么重转一次,直到指针指向一个标有数字的区域为止.写出下列事件发生的概率: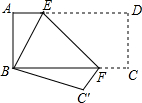 如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,△BC′F的周长是3.
如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,△BC′F的周长是3.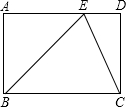 如图,在矩形ABCD中,∠ABC的平分线交AD于点E,连接CE.若BC=7,AE=4,则CE=5.
如图,在矩形ABCD中,∠ABC的平分线交AD于点E,连接CE.若BC=7,AE=4,则CE=5.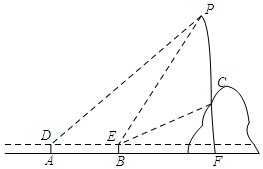 如图,从水平地面看一山坡上的通讯铁塔PC,在点A处用测角仪测得塔顶端点P的仰角是45°,向前走9m到达B点,用测角仪测得塔顶端点P和塔底端点C的仰角分别是60°和30°.
如图,从水平地面看一山坡上的通讯铁塔PC,在点A处用测角仪测得塔顶端点P的仰角是45°,向前走9m到达B点,用测角仪测得塔顶端点P和塔底端点C的仰角分别是60°和30°.