题目内容
8.如果a、b为定值时,关于x的方程$\frac{2kx+a}{3}$=2+$\frac{x-bk}{6}$,无论k取何值时,它的根总是1,则a=$\frac{13}{2}$,b=-4.分析 把x=1代入$\frac{2kx+a}{3}$=2+$\frac{x-bk}{6}$得:$\frac{2k+a}{3}$=2+$\frac{1-bk}{6}$,整理可得(4+b)k+2a-13=0,再由题意可得4+b=0,2a-13=0,再解即可.
解答 解:把x=1代入$\frac{2kx+a}{3}$=2+$\frac{x-bk}{6}$得:
$\frac{2k+a}{3}$=2+$\frac{1-bk}{6}$,
4k+2a=12+1-bk,
4k+bk+2a-13=0,
(4+b)k+2a-13=0,
∵无论k取何值时,它的根总是1,
∴4+b=0,2a-13=0,
解得:b=-4,a=$\frac{13}{2}$.
故答案为:$\frac{13}{2}$;-4.
点评 本题主要考查方程解的定义,由k可以取任何值得到a和b的值是解题的关键.

练习册系列答案
相关题目
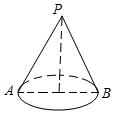 如图,这是某同学用纸板做成的一个底面直径为10cm,高为12cm的无底圆锥形玩具(接缝忽略不计),则做这个玩具所需纸板的面积是65πcm2(结果保留π).
如图,这是某同学用纸板做成的一个底面直径为10cm,高为12cm的无底圆锥形玩具(接缝忽略不计),则做这个玩具所需纸板的面积是65πcm2(结果保留π).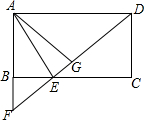 如图,四边形ABCD是矩形,点E在线段CB上,连接DE交AB的延长线于点F,∠AED=2∠CED,点G是DF中点,若BE=2,AG=2$\sqrt{7}$,则AB的长为2$\sqrt{6}$.
如图,四边形ABCD是矩形,点E在线段CB上,连接DE交AB的延长线于点F,∠AED=2∠CED,点G是DF中点,若BE=2,AG=2$\sqrt{7}$,则AB的长为2$\sqrt{6}$.
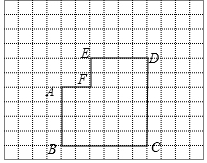 下列网格中的六边形ABCDEF是由边长为6的正方形左上角剪去边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.
下列网格中的六边形ABCDEF是由边长为6的正方形左上角剪去边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.