题目内容
9.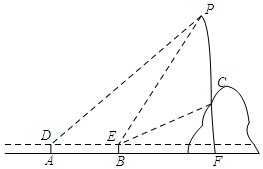 如图,从水平地面看一山坡上的通讯铁塔PC,在点A处用测角仪测得塔顶端点P的仰角是45°,向前走9m到达B点,用测角仪测得塔顶端点P和塔底端点C的仰角分别是60°和30°.
如图,从水平地面看一山坡上的通讯铁塔PC,在点A处用测角仪测得塔顶端点P的仰角是45°,向前走9m到达B点,用测角仪测得塔顶端点P和塔底端点C的仰角分别是60°和30°.(1)求∠BPC的度数.
(2)求该铁塔PF的高度,(结果精确到0.1m,参考数据:$\sqrt{3}≈1.73$.)
分析 (1)延长PC交直线AB于点G,根据直角三角形两锐角互余求得即可;
(2)设PE=x米,在直角△APE和直角△BPE中,根据三角函数利用x表示出AE和BE,根据AB=AE-BE即可列出方程求得x的值,再在直角△BCE中利用三角函数求得CE的长,则PF的长度即可求解.
解答 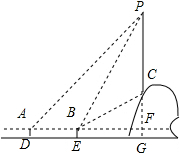 解:(1)延长PC交直线AB于点F,交直线DE于点G,则PF⊥AF,
解:(1)延长PC交直线AB于点F,交直线DE于点G,则PF⊥AF,
依题意得:∠PAF=45°,∠PBF=60°,∠CBF=30°
∴∠BPC=90°-60°=30°;
(2)根据题意得:AB=DE=9,FG=AD=1.3,
设PC=x m,则CB=CP=x,
在Rt△CBF中,BF=x•cos30°=$\frac{\sqrt{3}}{2}$x,CF=$\frac{1}{2}$x,
在Rt△APF中,FA=FP,
∴9+$\frac{\sqrt{3}}{2}$x=$\frac{1}{2}$x+x,x=9+3 $\sqrt{3}$,
∴PC=9+3 $\sqrt{3}$≈14.2,
∴PF=$\frac{1}{2}$x+x=21.3.
即该铁塔PF的高度约为21.3 m
点评 本题考查了仰角的定义、解直角三角形、三角函数;运用三角函数求出PE和QE是解决问题的关键.

练习册系列答案
相关题目
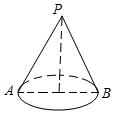 如图,这是某同学用纸板做成的一个底面直径为10cm,高为12cm的无底圆锥形玩具(接缝忽略不计),则做这个玩具所需纸板的面积是65πcm2(结果保留π).
如图,这是某同学用纸板做成的一个底面直径为10cm,高为12cm的无底圆锥形玩具(接缝忽略不计),则做这个玩具所需纸板的面积是65πcm2(结果保留π).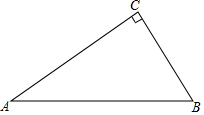 如图.△ABC是直角三角形,∠ACB=90°,∠A=30°.
如图.△ABC是直角三角形,∠ACB=90°,∠A=30°.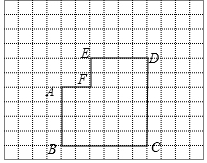 下列网格中的六边形ABCDEF是由边长为6的正方形左上角剪去边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.
下列网格中的六边形ABCDEF是由边长为6的正方形左上角剪去边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.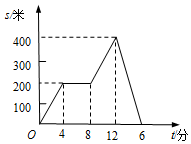 小明从家出发,外出散步,到一个公共阅报栏前看了一会儿报后,继续散步一段时间,然后回家.图中描述了小明在散步过程中到家的距离s(m)与散步所用时间t(min)之间的函数关系,则小明看报用了4min;小明返回家时的平均速度是100m/min.
小明从家出发,外出散步,到一个公共阅报栏前看了一会儿报后,继续散步一段时间,然后回家.图中描述了小明在散步过程中到家的距离s(m)与散步所用时间t(min)之间的函数关系,则小明看报用了4min;小明返回家时的平均速度是100m/min.