题目内容
3. 由菱形ABCD向外作四个正方形,若菱形ABCD与八边形的面积之比为1:11,则这个八边形每个内角的度数分别是105°,165°.
由菱形ABCD向外作四个正方形,若菱形ABCD与八边形的面积之比为1:11,则这个八边形每个内角的度数分别是105°,165°.
分析 连接AC,BD,根据菱形的性质得到AD=AB=CD=BC,∠DAB+∠ADC=180°,根据正方形的性质得到AA1=AA2=AD=AB=DD2=DD1,∠A2AB=∠A1AD=∠D1DC=90°,推出△A1AA2≌△ADC,同理△2CC1≌△ADC,△B1BB2≌△ADB≌△D1DD2,于是得到S${\;}_{正方形{A}_{1}AD{D}_{2}}$=2S菱形ABCD,过D作DE⊥AB与E,设菱形的边长为a,得到DE=$\frac{1}{2}$AD,求得∠DAB=30°,得到∠ADC=150°,于是得到结论.
解答 解:连接AC,BD,
∵四边形ABCD是菱形,
∴AD=AB=CD=BC,∠DAB+∠ADC=180°,
∵四边形A1ADD2,四边形AA2B1B,四边形DD1C2C是正方形,
∴AA1=AA2=AD=AB=DD2=DD1,∠A2AB=∠A1AD=∠D1DC=90°,
∴∠A1AA2+∠DAB=180°,
∴∠A1AA2=∠ADC,
在△A1AA2与△ADC中,$\left\{\begin{array}{l}{A{A}_{1}=AD}\\{∠{A}_{1}A{A}_{2}=∠ADC}\\{A{A}_{2}=AB}\end{array}\right.$,
∴△A1AA2≌△ADC,
同理△2CC1≌△ADC,△B1BB2≌△ADB≌△D1DD2,
∴S${\;}_{△{A}_{1}A{A}_{2}}$+S${\;}_{△{C}_{1}C{C}_{2}}$+S${\;}_{{B}_{1}B{B}_{2}}$+S${\;}_{△{D}_{1}D{D}_{2}}$=2S菱形ABCD,
∵菱形ABCD与八边形的面积之比为1:11,
∴S${\;}_{正方形{A}_{1}AD{D}_{2}}$=2S菱形ABCD,
过D作DE⊥AB与E,
设菱形的边长为a,
∴S${\;}_{正方形{A}_{1}AD{D}_{2}}$=a2=2S菱形ABCD=2a•DE,
∴DE=$\frac{1}{2}$a,
∴DE=$\frac{1}{2}$AD,
∴∠DAB=30°,
∴∠ADC=150°,
∴∠A1AA2=150°,∠D2DD1=30°,
∴∠AA1A2=15°,∠DD2D1=75°,
∴八边形每个内角的度数分别是105°,165°.
点评 本题考查了正方形的性质,全等三角形的判定和性质,菱形的性质,正确的作出辅助线是解题的关键.

| A. | -3 | B. | 3 | C. | 7 | D. | -7 |
| A. | $\sqrt{13}$ | B. | -$\sqrt{13}$ | C. | $\frac{1}{\sqrt{13}}$ | D. | $\frac{1}{13}$ |
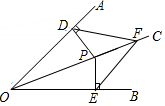 如图,OC是∠AOB的角平分线,点P、F在OC上,PD⊥AO于点D,PE⊥BO于点E,连接DF、EF.求证:DF=EF.
如图,OC是∠AOB的角平分线,点P、F在OC上,PD⊥AO于点D,PE⊥BO于点E,连接DF、EF.求证:DF=EF.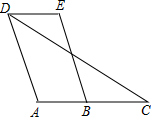 已知:如图,四边形ABCD中,点C在AB的延长线上,连接DC.∠EDC=∠C,AD∥BE.
已知:如图,四边形ABCD中,点C在AB的延长线上,连接DC.∠EDC=∠C,AD∥BE. 如图,在Rt△OAB中,∠ABO=90°,点O与原点重合,OB在数轴正半轴上,∠AOB=30°,AB=2,动点P从原点出发,在数轴正半轴上移动,当△OAP为等腰三角形时,P点表示的数是$\frac{4\sqrt{3}}{3}$或4或4$\sqrt{3}$.
如图,在Rt△OAB中,∠ABO=90°,点O与原点重合,OB在数轴正半轴上,∠AOB=30°,AB=2,动点P从原点出发,在数轴正半轴上移动,当△OAP为等腰三角形时,P点表示的数是$\frac{4\sqrt{3}}{3}$或4或4$\sqrt{3}$.