题目内容
5.解不等式组$\left\{\begin{array}{l}{2x+5≥3(x+2)}\\{\frac{2}{3}x>-5-x}\end{array}\right.$,并判断x=-$\frac{\sqrt{3}}{2}$是否满足该不等式组.分析 分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:解不等式2x+5≥3(x+2),得:x≤-1,
解不等式$\frac{2}{3}$x>-5-x,得:x>-3,
∴不等式组的解集为-3<x≤-1,
∵-$\frac{\sqrt{3}}{2}$>-1,
∴-$\frac{\sqrt{3}}{2}$不是该不等式组的解.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.在圆面积公式S=πR2中,变量是( )
| A. | S | B. | S与π | C. | S与R2 | D. | S与R |
13.下列命题中真命题的个数有( )
①小朋友荡秋千可以看做是平移运动;
②两条直线被第三条直线所截,同位角相等;
③过一点有且只有一条直线与已知直线平行;
④不是对顶角的角不相等.
①小朋友荡秋千可以看做是平移运动;
②两条直线被第三条直线所截,同位角相等;
③过一点有且只有一条直线与已知直线平行;
④不是对顶角的角不相等.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14. 菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )
菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )
 菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )
菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )| A. | (4,1) | B. | (4,-1) | C. | (1,4) | D. | (1,-4) |
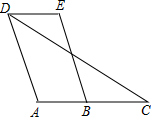 已知:如图,四边形ABCD中,点C在AB的延长线上,连接DC.∠EDC=∠C,AD∥BE.
已知:如图,四边形ABCD中,点C在AB的延长线上,连接DC.∠EDC=∠C,AD∥BE. 课间操时,小华、小军、小刚的位置如图,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成(4,3).
课间操时,小华、小军、小刚的位置如图,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成(4,3).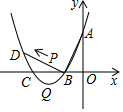 如图,已知抛物线y=x2+bx+c的顶点为Q,交y轴于点A(0,3),交x轴于B(-1,0),C两点,过点B作AB的垂线交抛物线于点D.
如图,已知抛物线y=x2+bx+c的顶点为Q,交y轴于点A(0,3),交x轴于B(-1,0),C两点,过点B作AB的垂线交抛物线于点D.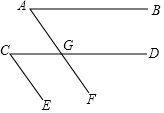 已知,如图:AB∥CD,若∠A的度数是x度,∠C的度数是y度,且x,y满足x2+y2=2xy,CE∥AF吗?为什么?
已知,如图:AB∥CD,若∠A的度数是x度,∠C的度数是y度,且x,y满足x2+y2=2xy,CE∥AF吗?为什么?