题目内容
已知抛物线y=-x2+bx+c经过点A(3,0),B(-1,0).
(1)求抛物线的解析式;
(2)若点A(0,y1),B(1,y2)都在该抛物线上,试比较y1与y2的大小.
(1)求抛物线的解析式;
(2)若点A(0,y1),B(1,y2)都在该抛物线上,试比较y1与y2的大小.
考点:待定系数法求二次函数解析式,二次函数图象上点的坐标特征
专题:
分析:(1)把点A、B的坐标代入函数解析式,根据待定系数法列式求解即可.
(2)先求得函数的对称轴为x=2,再判断A(0,y1),B(1,y2)在对称轴左侧,从而判断出y1与y2的大小关系.
(2)先求得函数的对称轴为x=2,再判断A(0,y1),B(1,y2)在对称轴左侧,从而判断出y1与y2的大小关系.
解答:解:(1)∵抛物线y=x2+bx+c经过点A(3,0),B(-1,0),
∴
,
解得:
,
∴抛物线的解析式是:y=-x2+4x-3.
(2)∵函数y=-x2+4x-3的对称轴为x=2,
∴A(0,y1),B(1,y2)在对称轴左侧,
∴抛物线开口向下,在对称轴左侧y随x的增大而增大.
∵0<1,
∴y1<y2.
∴
|
解得:
|
∴抛物线的解析式是:y=-x2+4x-3.
(2)∵函数y=-x2+4x-3的对称轴为x=2,
∴A(0,y1),B(1,y2)在对称轴左侧,
∴抛物线开口向下,在对称轴左侧y随x的增大而增大.
∵0<1,
∴y1<y2.
点评:此题考查了待定系数法求二次函数解析式,二次函数图象上点的特征,利用已知解析式得出对称轴进而利用二次函数增减性得出是解题关键.

练习册系列答案
相关题目
 如图,在等腰Rt△ABC中,∠ABC=90°,AB=BC,D为斜边AC延长线上一点,过D点作BC的垂线交其延长线于点E,在AB的延长线上取一点F,使得BF=CE,连接EF.
如图,在等腰Rt△ABC中,∠ABC=90°,AB=BC,D为斜边AC延长线上一点,过D点作BC的垂线交其延长线于点E,在AB的延长线上取一点F,使得BF=CE,连接EF.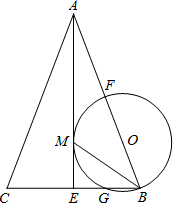 如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.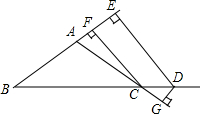 如图,已知AB=AC,DE⊥BA的延长线于E,DG⊥AC的延长线于点G,CF⊥BC于点F,试探索DE和CF+DG的关系.
如图,已知AB=AC,DE⊥BA的延长线于E,DG⊥AC的延长线于点G,CF⊥BC于点F,试探索DE和CF+DG的关系.