题目内容
15.在平面直角坐标系xOy中,△ABC的顶点坐标分别是A(x1,y1),B(x2,y2),C(x3,y3),对于△ABC的横长、纵长、纵横比给出如下定义:将|x1-x2|,|x2-x3|,|x3-x1|中的最大值,称为△ABC的横长,记作Dx;将|y1-y2|,|y2-y3|,|y3-y1|中的最大值,称为△ABC的纵长,记作Dy;将$\frac{{D}_{y}}{{D}_{x}}$叫做△ABC的纵横比,记作λ=$\frac{{D}_{y}}{{D}_{x}}$.
例如:如图1,△ABC的三个顶点的坐标分别是A(0,3),B(2,1),C(-1,-2),则Dx=|2-(-1)|=3,Dy=|3-(-2)|=5,
所以λ=$\frac{{D}_{y}}{{D}_{X}}$=$\frac{5}{3}$.
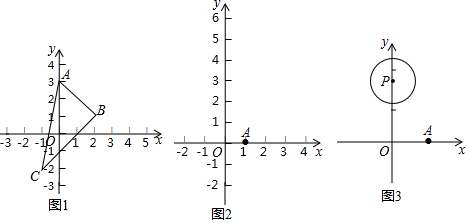
(1)如图2,点A(1,0),
①点B(2,1),E(-1,2),
则△AOB的纵横比λ1=$\frac{1}{2}$
△AOE的纵横比λ2=1;
②点F在第四象限,若△AOF的纵横比为1,写出一个符合条件的点F的坐标;
③点M是双曲线y=$\frac{1}{2x}$上一个动点,若△AOM的纵横比为1,求点M的坐标;
(2)如图3,点A(1,0),⊙P以P(0,$\sqrt{3}$)为圆心,1为半径,点N是⊙P上一个动点,直接写出△AON的纵横比λ的取值范围.
分析 (1)①根据纵横比的定义计算即可;
②点F在第四象限的角平分线上即可;
③分三种情形讨论即可.
(2)如图3中,当N(0,1+$\sqrt{3}$)时,可得△AON的纵横比λ的最大值=$\frac{1+\sqrt{3}}{1}$=1+$\sqrt{3}$,当AN′与⊙P相切时,切点在第二象限时,可得△AON的纵横比λ的最小值;
解答 解:(1)
由题意△AOB的纵横比λ1=$\frac{1}{2}$,△AOE的纵横比λ2=$\frac{2}{2}$=1,
故答案为$\frac{1}{2}$,1.
②由点F在第四象限,若△AOF的纵横比为1,则F(1,-1)(在第四象限的角平分线上即可).
③如图设M(xM,yM).
a、当0<xM≤1时,点M在y=$\frac{1}{2x}$上,则yM>0,
此时△AOM的横长Dx=1,△AOM的纵长为Dy=yM,
∵△AOM的纵横比为1,
∴Dy=1,
∴yM=1或-1(舍弃),
∴xM=$\frac{1}{2}$,
∴M($\frac{1}{2}$,1).
b、当xM>1时,点M在y=$\frac{1}{2x}$上,则yM>0,
此时△AOM的横长Dx=xM,△AOM的纵长为Dy=yM,
∵△AOM的纵横比为1,
∴Dy=Dx,
∴xM=yM
∴yM=±$\frac{\sqrt{2}}{2}$(舍弃),
c、当xM<0时,点M在y=$\frac{1}{2x}$上,则yM<0,
此时△AOM的横长Dx=1-xM,△AOM的纵长为Dy=-yM,
∵△AOM的纵横比为1,
∴1-xM=-yM,
∴xM=$\frac{1-\sqrt{3}}{2}$或$\frac{1+\sqrt{3}}{2}$(舍弃),
∴yM=-$\frac{1+\sqrt{3}}{2}$,
∴M′($\frac{1-\sqrt{3}}{2}$,-$\frac{1+\sqrt{3}}{2}$),
综上所述,点M坐标为($\frac{1}{2}$,1)或($\frac{1-\sqrt{3}}{2}$,-$\frac{1+\sqrt{3}}{2}$).
(2)如图3中,当N(0,1+$\sqrt{3}$)时,可得△AON的纵横比λ的最大值=$\frac{1+\sqrt{3}}{1}$=1+$\sqrt{3}$,
当AN′与⊙P相切时,切点在第二象限时,可得△AON的纵横比λ的最小值,
∵OP=$\sqrt{3}$,OA=1,
∴PA=2.AN′=$\sqrt{P{A}^{2}-PN{′}^{2}}$=$\sqrt{3}$,
∴tan∠APN′=$\sqrt{3}$,
∴∠APN′=60°,易知∠APO=30°,作N′H⊥OP于H.
∴∠HPN′=30°,
∴N′H=$\frac{1}{2}$,PH=$\frac{\sqrt{3}}{2}$,
此时△AON的纵横比λ=$\frac{\frac{\sqrt{3}}{2}}{\frac{3}{2}}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{\sqrt{3}}{3}$≤λ≤1+$\sqrt{3}$.
点评 本题考查反比例函数综合题、三角形的横长、纵长、纵横比λ的定义、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考创新题目.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{5}{2}$ | B. | -$\frac{3}{2}$ | C. | 3 | D. | $\frac{3}{2}$ |
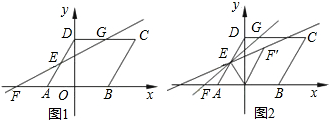
 已知抛物线y=a(x+1)2+k交x轴于A、B两点(点A在点B左侧),AB=4,顶点E在x轴上方,tan∠EAB=2.
已知抛物线y=a(x+1)2+k交x轴于A、B两点(点A在点B左侧),AB=4,顶点E在x轴上方,tan∠EAB=2.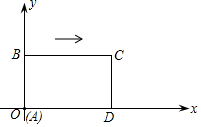 如图所示,在直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=5.若矩形以每秒2个单位长度沿x轴正方向作匀速运动,设运动时间为t(秒).
如图所示,在直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=5.若矩形以每秒2个单位长度沿x轴正方向作匀速运动,设运动时间为t(秒).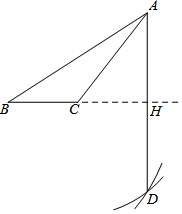 如图,已知钝角△ABC,老师按照如下步骤尺规作图:
如图,已知钝角△ABC,老师按照如下步骤尺规作图:
 如图,在三角形ABC中,AD为中线,AB=4,AC=2,AD为整数,求AD的长.
如图,在三角形ABC中,AD为中线,AB=4,AC=2,AD为整数,求AD的长.