题目内容
7.如果关于x的二次函数y=x2-2x+p的图象与端点为(-1,2)和(3,5)的线段只有一个交点,则p的值可能为( )| A. | $\frac{5}{2}$ | B. | -$\frac{3}{2}$ | C. | 3 | D. | $\frac{3}{2}$ |
分析 由二次函数y=x2-2x+p可知对称轴为x=-$\frac{b}{2a}$=1,根据题意抛物线可知经过点(-1,2)时,抛物线与线段有一个交点,代入(-1,2)即可求得p的可能值.
解答 解:∵二次函数y=x2-2x+p,
∴抛物线的对称轴为x=-$\frac{b}{2a}$=1,
∴抛物线经过点(-1,2)时,抛物线与线段有一个交点,
代入(-1,2)得,2=1-2+p,
∴p=3,
故选C.
点评 本题考查了二次函数的图象和二次函数的性质,求得抛物线的对称轴为x=-$\frac{b}{2a}$=1是解题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
18. 如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
 如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )| A. | 四边形ACDF是平行四边形 | |
| B. | 当点E为BC中点时,四边形ACDF是矩形 | |
| C. | 当点B与点E重合时,四边形ACDF是菱形 | |
| D. | 四边形ACDF不可能是正方形 |
2.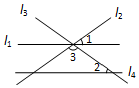 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=∠2=36°,则∠3的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=∠2=36°,则∠3的度数为( )
 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=∠2=36°,则∠3的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=∠2=36°,则∠3的度数为( )| A. | 60° | B. | 90° | C. | 108° | D. | 150° |

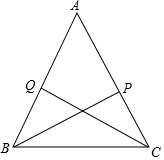 如图,CQ和BP是△ABC的角平分线,且BQ=CP,求证:AB=AC.
如图,CQ和BP是△ABC的角平分线,且BQ=CP,求证:AB=AC.