题目内容
10.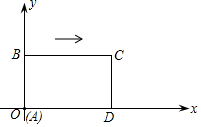 如图所示,在直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=5.若矩形以每秒2个单位长度沿x轴正方向作匀速运动,设运动时间为t(秒).
如图所示,在直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=5.若矩形以每秒2个单位长度沿x轴正方向作匀速运动,设运动时间为t(秒).(1)当t=4时,写出B点的坐标;
(2)若在矩形运动的同时点P从A点出发,以每秒1个单位长度沿A-B-C-D的路线作匀速运动,当P点运动到D点时停止运动,矩形ABCD也随之停止运动.
①当t=4时,求出点P的坐标;
②若△OAP的面积为S,试求出S与t之间的函数关系式(并写出自变量t的取值范围)
分析 (1)由于B(0,3),根据平移法则即可得出结论;
(2)①先判断出先P在边BC上,向右移动的单位数即可得出结论;
②分三种情况利用三角形的面积公式即可求解.
解答 解:(1)∵矩形ABCD,AB=3,AD=5,∴B(0,3),∵矩形以每秒2个单位长度沿x轴正方向平移了2×4=8个单位长度,∴当t=4时,B(8,3);
(2)①当t=4时,P点从A点运动到BC上,
过点P作PE⊥AD于点E.
此时A点到E点的时间=8秒,AB+BP=4,
∴BP=1 则PE=AB=3,AE=BP=1
则PE=AB=3,AE=BP=1
∴OE=OA+AE=8+1=9
∴点P的坐标为(9,3);
②当②分三种情况:
i.0<t≤3时,点P在AB上运动,此时OA=2t,AP=t
∴S=$\frac{1}{2}$×2t×t=t2
ii.3<t≤8时,点P在BC上运动,此时OA=2t
∴S=$\frac{1}{2}$×2t×3=3t
iii.8<t<11时,点P在CD上运动,此时OA=2t,AB+BC+CP=t
∴DP=(AB+BC+CD)-(AB+BC+CP)=11-t
∴S=$\frac{1}{2}$×2t×(11-t)=-t2+11t
综上所述,s与t之间的函数关系式是:
当0<t≤3时,s=t2;
当3<t≤8时,s=3t;
当8<t<11时,s=-t2+11t;
综上所述,S与t之间的函数关系式是:
当0<t≤3时,S=t2;
当3<t≤8时,S=3t;
当8<t<11时,S=-t2+11t.
点评 此题是四边形综合题,主要考查了平移的特点,三角形的面积公式,解本题的关键是(2)②分类讨论的思想解决问题,是一道比较简单的中考常考题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
1.设等腰三角形底角的度数x(单位:度)为自变量,顶角的度数y为因变量,则y与x的函数关系式为( )
| A. | y=180-2x(0<x<90) | B. | y=90-x(0≤x≤90) | C. | y=180-x(0<x<90) | D. | y=90-2x(0≤x≤90) |
18. 如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
 如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )| A. | 四边形ACDF是平行四边形 | |
| B. | 当点E为BC中点时,四边形ACDF是矩形 | |
| C. | 当点B与点E重合时,四边形ACDF是菱形 | |
| D. | 四边形ACDF不可能是正方形 |
2.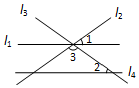 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=∠2=36°,则∠3的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=∠2=36°,则∠3的度数为( )
 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=∠2=36°,则∠3的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=∠2=36°,则∠3的度数为( )| A. | 60° | B. | 90° | C. | 108° | D. | 150° |
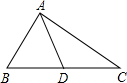 如图,在△ABC中,AD是BC边上的中线,若AB=3cm,AC=5cm,则AD的取值范围是1cm<AD<4cm.
如图,在△ABC中,AD是BC边上的中线,若AB=3cm,AC=5cm,则AD的取值范围是1cm<AD<4cm.