题目内容
20.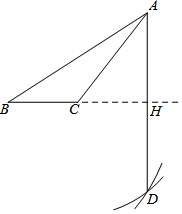 如图,已知钝角△ABC,老师按照如下步骤尺规作图:
如图,已知钝角△ABC,老师按照如下步骤尺规作图:步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H.
小明说:图中的BH⊥AD且平分AD.
小丽说:图中AC平分∠BAD.
小强说:图中点C为BH的中点.
他们的说法中正确的是小明.他的依据是到线段两个端点距离相等的点在线段的垂直平分线上;两点确定一条直线.
分析 根据已知条件可知,直线BC是线段AD的垂直平分线,由此一一判断各说法即可.
解答  解:如图,连接CD、BD,
解:如图,连接CD、BD,
∵CA=CD,BA=BD,
∴点C、点B在线段AD的垂直平分线上,
∴直线BC是线段AD的垂直平分线,
即BH⊥AD且平分AD,故小明的说法正确.
而CA不一定平分∠BDA,故小丽的说法错误;点C不一定为BH的中点,故小强的说法错误.
故答案为:小明;到线段两个端点距离相等的点在线段的垂直平分线上;两点确定一条直线.
点评 本题考查作图-基本作图、线段的垂直平分线的性质等知识,解题的关键是掌握:线段垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
11.如果a<b,那么下列不等式中一定成立的是( )
| A. | a2<ab | B. | ab<b2 | C. | a2<b2 | D. | a-2b<-b |
5.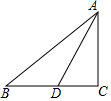 如图,在Rt△ABC中,∠ACB=90°,AD是BC边上的中线,如果AD=BC,那么tan∠B的值是( )
如图,在Rt△ABC中,∠ACB=90°,AD是BC边上的中线,如果AD=BC,那么tan∠B的值是( )
 如图,在Rt△ABC中,∠ACB=90°,AD是BC边上的中线,如果AD=BC,那么tan∠B的值是( )
如图,在Rt△ABC中,∠ACB=90°,AD是BC边上的中线,如果AD=BC,那么tan∠B的值是( )| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |