题目内容
5. 如图,在△ABC中,cosB=$\frac{\sqrt{2}}{2}$,sinC=$\frac{3}{5}$,AC=10,则△ABC的面积为42.
如图,在△ABC中,cosB=$\frac{\sqrt{2}}{2}$,sinC=$\frac{3}{5}$,AC=10,则△ABC的面积为42.
分析 过点A作AC⊥BC于点D,根据锐角三角函数的定义,求出AD、BD和CD的长度.
解答 解:过点A作AC⊥BC于点D,
∵sinC=$\frac{AD}{AC}$,
∴AD=AC•sinC=6,
∴由勾股定理可知:BC=8,
∵cosB=$\frac{\sqrt{2}}{2}$,
∴∠B=45°,
∴BD=AD=6,
∴BC=14
∴△ABC的面积为:$\frac{1}{2}$BC•AD=$\frac{1}{2}$×6×14=42
故答案为:42
点评 本题考查解直角三角形,解题的关键是根据锐角三角函数求出AD与BD的长度,本题属于基础题型.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
10.若a与b互为相反数,则|a+b-2|等于( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
17.已知y是x的一次函数,下表中给出了x与y的部分对应值,则m的值是-9.
| x | -1 | 2 | 6 |
| y | 5 | -1 | m |
15.下列方程中,解是x=3的是( )
| A. | 3x=1 | B. | 2x-6=0 | C. | 3x+9=0 | D. | $\frac{1}{3}$x=0 |
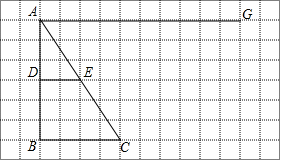 如图,在网格图中,有△ABC与线段DE,在线段AG上是否存在点M,使得△MEC与△ADE相似?若存在,请先在图中确定出所有的点M,并选择其中一个说明理由;若不存在,也请说明理由.(图中各点均在格点上).
如图,在网格图中,有△ABC与线段DE,在线段AG上是否存在点M,使得△MEC与△ADE相似?若存在,请先在图中确定出所有的点M,并选择其中一个说明理由;若不存在,也请说明理由.(图中各点均在格点上).