题目内容
2.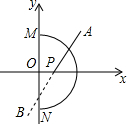 如图,在平面直角坐标系中,以原点O为圆心,3为半径的半圆,直线AB:y=x+b与x轴交于点P(x,0),若直线AB与半圆弧有公共点,则x值的范围是( )
如图,在平面直角坐标系中,以原点O为圆心,3为半径的半圆,直线AB:y=x+b与x轴交于点P(x,0),若直线AB与半圆弧有公共点,则x值的范围是( )| A. | -3≤x≤3$\sqrt{2}$ | B. | -3≤x≤3 | C. | -3$\sqrt{2}$≤x≤3 | D. | 0≤x≤3$\sqrt{2}$ |
分析 作OH⊥AB于H,如图,则OP=|x|,∠OPH=45°,利用等腰直角三角形的性质得OH=$\frac{\sqrt{2}}{2}$|x|,根据题意可判断直线AB与圆相交或相切,所以$\frac{\sqrt{2}}{2}$|x|≤3,然后解绝对值不等式即可,直线经过点M时OP的值即可.
解答 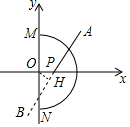 解:作OH⊥AB于H,如图,
解:作OH⊥AB于H,如图,
∵直线AB:y=x+b,
∴tan∠OHB=$\frac{OB}{OP}$=1,
∴∠OPH=45°
∵OP=|x|,
∴OH=$\frac{\sqrt{2}}{2}$|x|,
∵AB与⊙O有公共点,
∴OH≤3,
即$\frac{\sqrt{2}}{2}$|x|≤3,
当直线与半圆相切时,OP=3$\sqrt{2}$,直线经过M时,OP=3,
∴-3≤x≤3$\sqrt{2}$,
故选A.
点评 本题考查了直线与圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,若直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.解决本题的关键是用P点的横坐标表示点O到直线AB的距离.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.若a与b互为相反数,则|a+b-2|等于( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
17.已知y是x的一次函数,下表中给出了x与y的部分对应值,则m的值是-9.
| x | -1 | 2 | 6 |
| y | 5 | -1 | m |
11.正比例函数y=x的图象与反比例函数y=$\frac{1}{x}$的图象的交点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第一、三象限 |
12.如果$\frac{y}{x}$=2017,则$\frac{y-x}{-x}$等于( )
| A. | 2017 | B. | -2017 | C. | 2016 | D. | -2016 |
 已知.
已知.