题目内容
一个不透明的袋子中装有大小、质地完全相同的3只球,球上分别标有2,3,5三个数字.从这个袋子中任意摸一只球,记下所标数字,不放回,再从从这个袋子中任意摸一只球,记下所标数字.将第一次记下的数字作为十位数字,第二次记下的数字作为个位数字,组成一个两位数.则组成的两位数是5的倍数的概率为 .
考点:列表法与树状图法
专题:计算题
分析:列表得出所有等可能的结果,找出组成的两位数是5的倍数的情况,即可求出所求的概率.
解答:解:列表得:
所有等可能的情况有6种,其中组成两位数是5的倍数的情况有2种,
则P=
=
.
故答案为:
| 2 | 3 | 5 | |
| 2 | --- | (3,2) | (5,2) |
| 3 | (2,3) | --- | (5,3) |
| 5 | (2,5) | (3,5) | --- |
则P=
| 2 |
| 6 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
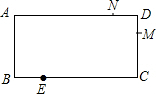 如图,矩形ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以3cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动,当动点M回到点D时,M、N两点均停止运动.
如图,矩形ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以3cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动,当动点M回到点D时,M、N两点均停止运动.
 在△ABC中,AB=AC,CD=CB,若∠ACD=42°,则∠BAC=
在△ABC中,AB=AC,CD=CB,若∠ACD=42°,则∠BAC= 如图是一把剪刀的局部示意图,刀片内沿在AB、CD上,EF是刀片外沿.AB、CD相交于点N,EF、CD相交于点M,刀片宽MH=1.5cm.小丽在使用这把剪刀时,∠ANC不超过30°.若想一刀剪断4cm宽的纸带,则刀身AH长至少为
如图是一把剪刀的局部示意图,刀片内沿在AB、CD上,EF是刀片外沿.AB、CD相交于点N,EF、CD相交于点M,刀片宽MH=1.5cm.小丽在使用这把剪刀时,∠ANC不超过30°.若想一刀剪断4cm宽的纸带,则刀身AH长至少为 如图,在?ABCD中,E为BC边上一点(不与端点重合),若AB=AE,且AE平分
如图,在?ABCD中,E为BC边上一点(不与端点重合),若AB=AE,且AE平分 已知A,B两地间有汽车站C,客车由A地驶向C站、货车由B地经过C站去A地(客货车在A,C两地间沿同一条路行驶),两车同时出发,匀速行驶,(中间不停留)货车的速度是客车速度的
已知A,B两地间有汽车站C,客车由A地驶向C站、货车由B地经过C站去A地(客货车在A,C两地间沿同一条路行驶),两车同时出发,匀速行驶,(中间不停留)货车的速度是客车速度的