题目内容
9.已知关于x的不等式组$\left\{\begin{array}{l}{\frac{x-3}{2}≤x-1}\\{\frac{x-1}{3}>x-a}\end{array}\right.$的整数解共有2个,求a的取值范围.分析 先分别解两个不等式得到不等式组的解集为-1≤x≤$\frac{3a-1}{2}$,则可确定不等式组的整数解为-1,0,于是可得到a不等式组,解不等式组可得a的范围.
解答 解:解不等式$\frac{x-3}{2}$≤x-1,得:x≥-1,
解不等式$\frac{x-1}{3}$>x-a,得:x≤$\frac{3a-1}{2}$,
∵不等式组的整数解共有2个,
∴0≤$\frac{3a-1}{2}$<1,
解得:$\frac{1}{3}$≤a<1.
点评 本题考查了一元一次不等式组的整数解:已知解集(整数解)求字母的取值.一般思路为:先把题目中除未知数外的字母当做常数看待解不等式组或方程组等,然后再根据题目中对结果的限制的条件得到有关字母的代数式,最后解代数式即可得到答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列运算正确的是( )
| A. | a+a=2a2 | B. | a2•a=2a2 | C. | (-ab)2=2ab2 | D. | (2a)2÷a=4a |
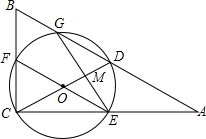 如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O分别交边AB、BC,AC于点G,F,E,GE交CD于点M,ME=4$\sqrt{6}$,MD:CO=2:5.
如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O分别交边AB、BC,AC于点G,F,E,GE交CD于点M,ME=4$\sqrt{6}$,MD:CO=2:5.