题目内容
17.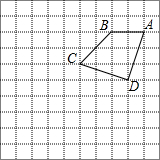 如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.
如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.(1)在图中画出四边形AB′C′D′;
(2)填空:△AC′D′是等腰直角三角形.
分析 (1)延长AB到B′,使AB′=2AB,得到B的对应点B′,同样得到C、D的对应点C′,D′,再顺次连接即可;
(2)利用勾股定理求出AC′2=42+82=80,AD′2=62+22=40,C′D′2=62+22=40,那么AD′=C′D′,AD′2+C′D′2=AC′2,即可判定△AC′D′是等腰直角三角形.
解答 解:(1)如图所示:
(2)∵AC′2=42+82=16+64=80,AD′2=62+22=36+4=40,C′D′2=62+22=36+4=40,
∴AD′=C′D′,AD′2+C′D′2=AC′2,
∴△AC′D′是等腰直角三角形.
故答案为:等腰直角.
点评 本题考查了作图-位似变换.画位似图形的一般步骤为:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形.同时考查了勾股定理及其逆定理等知识.熟练掌握网格结构以及位似变换的定义是解题的关键.

练习册系列答案
相关题目
7.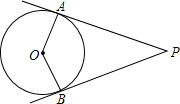 如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )
如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )
 如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )
如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )| A. | 150° | B. | 130° | C. | 155° | D. | 135° |
8.若代数式$\frac{1}{x-1}$+$\sqrt{x}$有意义,则实数x的取值范围是( )
| A. | x≠1 | B. | x≥0 | C. | x≠0 | D. | x≥0且x≠1 |
2.若关于x的分式方程$\frac{m-1}{x-1}$=2的解为非负数,则m的取值范围是( )
| A. | m>-1 | B. | m≥1 | C. | m>-1且m≠1 | D. | m≥-1且m≠1 |
6.已知a2+2a=1,则代数式2a2+4a-1的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | -2 |
 均匀地向如图的容器中注满水,能反映在注水过程中水面高度h随时间t变化的函数图象是( )
均匀地向如图的容器中注满水,能反映在注水过程中水面高度h随时间t变化的函数图象是( )



 如图是根据某公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点A(400,300),从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向左转90°后直行400m到达梅花阁C,则点C的坐标是(400,800).
如图是根据某公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点A(400,300),从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向左转90°后直行400m到达梅花阁C,则点C的坐标是(400,800).