题目内容
9. 如图是根据某公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点A(400,300),从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向左转90°后直行400m到达梅花阁C,则点C的坐标是(400,800).
如图是根据某公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点A(400,300),从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向左转90°后直行400m到达梅花阁C,则点C的坐标是(400,800).
分析 根据题意结合全等三角形的判定与性质得出△AOD≌△ACB(SAS),进而得出C,A,D也在一条直线上,求出CD的长即可得出C点坐标.
解答  解:连接AC,
解:连接AC,
由题意可得:AB=300m,BC=400m,
在△AOD和△ACB中
∵$\left\{\begin{array}{l}{AD=AB}\\{∠ODA=∠ABC}\\{DO=BC}\end{array}\right.$,
∴△AOD≌△ACB(SAS),
∴∠CAB=∠OAD,
∵B、O在一条直线上,
∴C,A,D也在一条直线上,
∴AC=AO=500m,则CD=AC=AD=800m,
∴C点坐标为:(400,800).
故答案为:(400,800).
点评 此题主要考查了全等三角形的判定与性质以及勾股定理,得出C,A,D也在一条直线上是解题关键.

练习册系列答案
相关题目
19.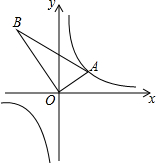 如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=$\frac{1}{x}$的图象上.若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=$\frac{1}{x}$的图象上.若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
 如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=$\frac{1}{x}$的图象上.若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=$\frac{1}{x}$的图象上.若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )| A. | -4 | B. | 4 | C. | -2 | D. | 2 |
20.下列调查中,适宜采用普查方式的是( )
| A. | 了解一批圆珠笔的寿命 | |
| B. | 了解全国九年级学生身高的现状 | |
| C. | 考察人们保护海洋的意识 | |
| D. | 检查一枚用于发射卫星的运载火箭的各零部件 |
14.函数y=$\frac{1}{\sqrt{x-2}}$+x-2的自变量x的取值范围是( )
| A. | x≥2 | B. | x>2 | C. | x≠2 | D. | x≤2 |
1.若|a-1|=a-1,则a的取值范围是( )
| A. | a≥1 | B. | a≤1 | C. | a<1 | D. | a>1 |
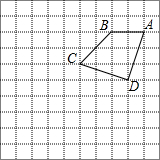 如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.
如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2. “为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)