题目内容
7.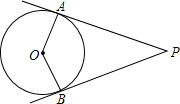 如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )
如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )| A. | 150° | B. | 130° | C. | 155° | D. | 135° |
分析 由PA与PB为圆的两条切线,利用切线性质得到PA与OA垂直,PB与OB垂直,在四边形APBO中,利用四边形的内角和定理即可求出∠AOB的度数.
解答 解:∵PA、PB是⊙O的切线,
∴PA⊥OA,PB⊥OB,
∴∠PAO=∠PBO=90°,
∵∠P=50°,
∴∠AOB=130°.
故选B.
点评 此题考查了切线的性质,以及四边形的内角和定理,熟练掌握切线的性质是解本题的关键.

练习册系列答案
相关题目
17. 某工厂生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本y(万元)与产量x(吨)之间是一次函数关系,函数y与自变量x的部分对应值如表:
某工厂生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本y(万元)与产量x(吨)之间是一次函数关系,函数y与自变量x的部分对应值如表:
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)当投入生产这种产品的总成本为1200万元时,求该产品的总产量;(注:总成本=每吨成本×总产量)
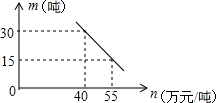
(3)市场调查发现,这种产品每月销售量m(吨)与销售单价n(万元/吨)之间满足如图所示的函数关系,该厂第一个月按同一销售单价卖出这种产品25吨.请求出该厂第一个月销售这种产品获得的利润.(注:利润=售价-成本)
 某工厂生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本y(万元)与产量x(吨)之间是一次函数关系,函数y与自变量x的部分对应值如表:
某工厂生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本y(万元)与产量x(吨)之间是一次函数关系,函数y与自变量x的部分对应值如表:| x(吨) | 10 | 20 | 30 |
| y(万元/吨) | 45 | 40 | 35 |
(2)当投入生产这种产品的总成本为1200万元时,求该产品的总产量;(注:总成本=每吨成本×总产量)
(3)市场调查发现,这种产品每月销售量m(吨)与销售单价n(万元/吨)之间满足如图所示的函数关系,该厂第一个月按同一销售单价卖出这种产品25吨.请求出该厂第一个月销售这种产品获得的利润.(注:利润=售价-成本)
2.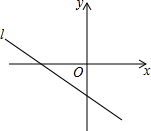 如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a可能在( )
如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a可能在( )
 如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a可能在( )
如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a可能在( )| A. | 1<a<2 | B. | -2<a<0 | C. | -3≤a≤-2 | D. | -10<a<-4 |
12.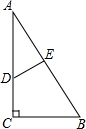 如图,在△ABC中,∠C=90°,点D,E分别在边AC,AB上.若∠B=∠ADE,则下列结论正确的是( )
如图,在△ABC中,∠C=90°,点D,E分别在边AC,AB上.若∠B=∠ADE,则下列结论正确的是( )
 如图,在△ABC中,∠C=90°,点D,E分别在边AC,AB上.若∠B=∠ADE,则下列结论正确的是( )
如图,在△ABC中,∠C=90°,点D,E分别在边AC,AB上.若∠B=∠ADE,则下列结论正确的是( )| A. | ∠A和∠B互为补角 | B. | ∠B和∠ADE互为补角 | ||
| C. | ∠A和∠ADE互为余角 | D. | ∠AED和∠DEB互为余角 |

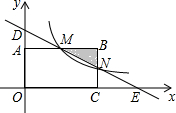 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标(4,2),过点D(0,3)和E(6,0)的直线分别于AB,BC交于点M,N.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标(4,2),过点D(0,3)和E(6,0)的直线分别于AB,BC交于点M,N.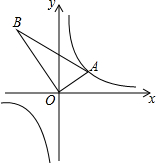 如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=$\frac{1}{x}$的图象上.若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=$\frac{1}{x}$的图象上.若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( ) 将全体正整数排成一个三角形数阵,根据上述排列规律,数阵中第10行从左至右的第5个数是50.
将全体正整数排成一个三角形数阵,根据上述排列规律,数阵中第10行从左至右的第5个数是50.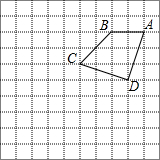 如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.
如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.