题目内容
12.若关于x的一元二次方程ax2+3x-1=0有两个不相等的实数根,则a的取值范围是a>-$\frac{9}{4}$且a≠0.分析 根据一元二次方程的定义及判别式的意义可得a≠0且△=b2-4ac=32-4×a×(-1)=9+4a>0,解不等式组即可求出a的取值范围.
解答 解:∵关于x的一元二次方程ax2+3x-1=0有两个不相等的实数根,
∴a≠0且△=b2-4ac=32-4×a×(-1)=9+4a>0,
解得:a>-$\frac{9}{4}$且a≠0.
故答案为:a>-$\frac{9}{4}$且a≠0.
点评 此题考查了根的判别式.一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.同时考查了一元二次方程的定义.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
2.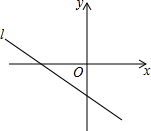 如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a可能在( )
如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a可能在( )
 如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a可能在( )
如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a可能在( )| A. | 1<a<2 | B. | -2<a<0 | C. | -3≤a≤-2 | D. | -10<a<-4 |
3.在-1,-2,0,1四个数中最小的数是( )
| A. | -1 | B. | -2 | C. | 0 | D. | 1 |
20.下列调查中,适宜采用普查方式的是( )
| A. | 了解一批圆珠笔的寿命 | |
| B. | 了解全国九年级学生身高的现状 | |
| C. | 考察人们保护海洋的意识 | |
| D. | 检查一枚用于发射卫星的运载火箭的各零部件 |
7.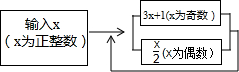 在数学活动课上,同学们利用如图的程序进行计算,发现无论x取任何正整数,结果都会进入循环,下面选项一定不是该循环的是( )
在数学活动课上,同学们利用如图的程序进行计算,发现无论x取任何正整数,结果都会进入循环,下面选项一定不是该循环的是( )
 在数学活动课上,同学们利用如图的程序进行计算,发现无论x取任何正整数,结果都会进入循环,下面选项一定不是该循环的是( )
在数学活动课上,同学们利用如图的程序进行计算,发现无论x取任何正整数,结果都会进入循环,下面选项一定不是该循环的是( )| A. | 4,2,1 | B. | 2,1,4 | C. | 1,4,2 | D. | 2,4,1 |
1.若|a-1|=a-1,则a的取值范围是( )
| A. | a≥1 | B. | a≤1 | C. | a<1 | D. | a>1 |
2.方程2x-1=3的解是( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
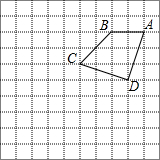 如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.
如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.