题目内容
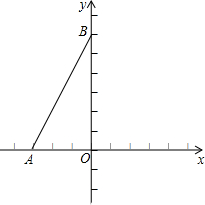 已知A(-3,0),B(0,6),通过原点O的直线把△OAB分为面积为1:3的两部分,求这条直线的函数解析式.
已知A(-3,0),B(0,6),通过原点O的直线把△OAB分为面积为1:3的两部分,求这条直线的函数解析式.考点:待定系数法求一次函数解析式
专题:分类讨论
分析:首先求得△ABC的面积,则△AOC和△OBC的面积即可求得,根据三角形的面积公式即可求得C的坐标,利用待定系数法求得直线的解析式.
解答: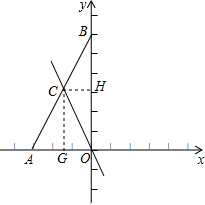 解:设直线y=kx+b,直线与AB边交于点C,
解:设直线y=kx+b,直线与AB边交于点C,
S△ABC=
OA•OB=
×3×6=9,
过C作CG⊥OA,CH⊥OB.
若S△OAC=
S△ABC=
,S△OBC=
S△ABC=
,
×3CG=
,CG=
,
×6CH=
,则CH=
.
则C的坐标是(-
,
),则解析式是y=-
x;
若S△OAC=
S△ABC=
,S△OBC=
S△ABC=
,
即
×3CG=
,CG=
,
,6CH=
,则CH=
.
则C的坐标是(-
,
),则函数解析式是y=-6x.
则函数解析式是:y=-
x或y=-6x.
 解:设直线y=kx+b,直线与AB边交于点C,
解:设直线y=kx+b,直线与AB边交于点C,S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
过C作CG⊥OA,CH⊥OB.
若S△OAC=
| 1 |
| 4 |
| 9 |
| 4 |
| 3 |
| 4 |
| 27 |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 27 |
| 4 |
| 9 |
| 4 |
则C的坐标是(-
| 9 |
| 4 |
| 3 |
| 2 |
| 2 |
| 3 |
若S△OAC=
| 3 |
| 4 |
| 27 |
| 4 |
| 1 |
| 4 |
| 9 |
| 4 |
即
| 1 |
| 2 |
| 27 |
| 4 |
| 9 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
| 3 |
| 4 |
则C的坐标是(-
| 3 |
| 4 |
| 9 |
| 2 |
则函数解析式是:y=-
| 2 |
| 3 |
点评:本题考查了待定系数法求函数的解析式,正确求得C的坐标是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
不等式
-
≥1的正整数解是( )
| x-1 |
| 6 |
| x-3 |
| 2 |
| A、0 | B、1 | C、0和1 | D、0或1 |
 如图,AB是⊙O的直径,PA,PC是⊙O的两条切线,连接CA.若AB=4,PC=6,则AC的长为( )
如图,AB是⊙O的直径,PA,PC是⊙O的两条切线,连接CA.若AB=4,PC=6,则AC的长为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
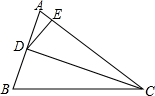 如图,CD是△ABC中∠ACB的平分线,E是AC上的一点,且CD2=BC•CE,AD=6,AE=4.
如图,CD是△ABC中∠ACB的平分线,E是AC上的一点,且CD2=BC•CE,AD=6,AE=4.