题目内容
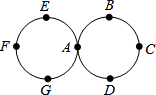 如图物体从点A出发,按照A→B(第1步)→C(第2步)→D→A→E→F→G→A→B→…的顺序循环运动,则第2015步到达点
如图物体从点A出发,按照A→B(第1步)→C(第2步)→D→A→E→F→G→A→B→…的顺序循环运动,则第2015步到达点考点:规律型:图形的变化类
专题:
分析:求出由A点开始按照A→B(第1步)→C(第2步)→D→A→E→F→G→A→B→…的顺序循环运动走一圈所走的步数,再用2015除以此步数即可.
解答:解:∵如图物体从点A出发,按照A→B(第1步)→C(第2步)→D→A→E→F→G→A→B→…的顺序循环运动,此时一个循环为8步,
∴2015÷8=251…7.
∴当物体走到第251圈后再走7步正好到达G点.
故答案为:G.
∴2015÷8=251…7.
∴当物体走到第251圈后再走7步正好到达G点.
故答案为:G.
点评:本题考查的是图形的变化规律,解答此题的关键是根据题意得出物体走一个循环的步数,找出规律即可解答.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
若∠A=20°18′,∠B=20°15″,∠C=20.25°,则有( )
| A、∠A>∠B>∠C |
| B、∠B>∠A>∠C |
| C、∠A>∠C>∠B |
| D、∠C>∠A>∠B |
 如图,在?ABCD中,对角线AC,BD相交于点O,点E,F是对角线AC上的两点,当点E,F满足下列条件时,四边形DEBF不一定是平行四边形( )
如图,在?ABCD中,对角线AC,BD相交于点O,点E,F是对角线AC上的两点,当点E,F满足下列条件时,四边形DEBF不一定是平行四边形( )| A、AE=CF |
| B、DE=BF |
| C、∠ADE=∠CBF |
| D、∠AED=∠CFB |
下列图案均是用长度相同的小木棒按一定的规律拼搭而成:拼搭第1个图案需4根小木棒,拼塔第2个图案需10根小木棒,…,依此规律,拼成第6个图案小木棒( )


| A、36根 | B、48根 |
| C、54根 | D、64根 |
 已知:如图,OB是∠AOC的角平分线,OC是∠AOD的角平分线,∠COD=70°,那么∠AOD的度数为
已知:如图,OB是∠AOC的角平分线,OC是∠AOD的角平分线,∠COD=70°,那么∠AOD的度数为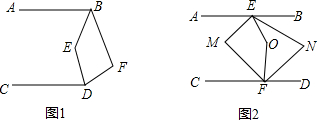
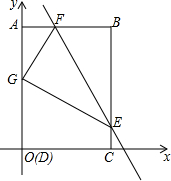 如图,四边形ABCD为矩形,C点在x轴上,A点在y轴上,D(0,0),B(3,4),矩形ABCD沿直线EF折叠,点B落在AD边上的G处,E,F分别在BC,AB边上且F(1,4).
如图,四边形ABCD为矩形,C点在x轴上,A点在y轴上,D(0,0),B(3,4),矩形ABCD沿直线EF折叠,点B落在AD边上的G处,E,F分别在BC,AB边上且F(1,4). 如图,点D、E是等边△ABC的BC、AC上的点,且CD=AE,AD、BE相交于P点,BQ⊥AD.
如图,点D、E是等边△ABC的BC、AC上的点,且CD=AE,AD、BE相交于P点,BQ⊥AD.