题目内容
15.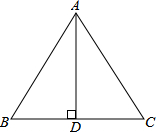 在等腰△ABC中,AB=AC=10cm,BC=12cm,求BC边上的高AD及△ABC的面积.
在等腰△ABC中,AB=AC=10cm,BC=12cm,求BC边上的高AD及△ABC的面积.
分析 利用等腰三角形的“三线合一”的性质得到BD=$\frac{1}{2}$BC=6cm,然后在直角△ABD中,利用勾股定理求得高线AD的长度,再根据三角形的面积公式计算即可求解.
解答  解:如图,AD是BC边上的高线.
解:如图,AD是BC边上的高线.
∵AB=AC=10 cm,BC=12cm,
∴BD=CD=6cm.
∴在Rt△ABD中,由勾股定理,得 AD=$\sqrt{A{B^2}-B{D^2}}$=$\sqrt{{{10}^2}-{6^2}}$=8(cm),
S△ABC=12×8÷2=48(cm2).
点评 本题主要考查了等腰三角形的三线合一定理和勾股定理.等腰三角形底边上的高线把等腰三角形分成两个全等的直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论正确的是( )
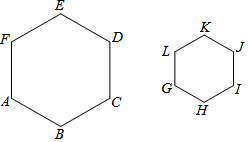

| A. | ∠B=2∠K | |
| B. | 六边形ABCDEF的周长=六边形GHIJKL的周长 | |
| C. | BC=2HI | |
| D. | S六边形ABCDEF=2S六边形GHIJKL |
10.下列各组数据不能作为直角三角形的三边长的是( )
| A. | 3,4,5 | B. | 6,8,10 | C. | 5,12,13 | D. | 13,16,18 |
20. 已知二次函数y=ax2+bx+c+2的图象如图所示,有下列4个结论:①abc<0;②b2=4ac;③a+c=b-2;④m(am+b)+b>a(m≠-1),其中结论正确的有( )
已知二次函数y=ax2+bx+c+2的图象如图所示,有下列4个结论:①abc<0;②b2=4ac;③a+c=b-2;④m(am+b)+b>a(m≠-1),其中结论正确的有( )
 已知二次函数y=ax2+bx+c+2的图象如图所示,有下列4个结论:①abc<0;②b2=4ac;③a+c=b-2;④m(am+b)+b>a(m≠-1),其中结论正确的有( )
已知二次函数y=ax2+bx+c+2的图象如图所示,有下列4个结论:①abc<0;②b2=4ac;③a+c=b-2;④m(am+b)+b>a(m≠-1),其中结论正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.化简$\sqrt{27}+\sqrt{48}$的结果是( )
| A. | $\sqrt{75}$ | B. | $5\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $7\sqrt{3}$ |
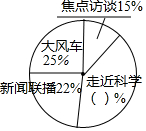 下面是六年级一班学生喜欢的电视节目统计图.
下面是六年级一班学生喜欢的电视节目统计图.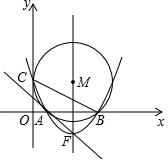 如图,在平面直角坐标系中,点M的坐标是(5,4),⊙M与y轴相切于点C,与x轴相交于A,B两点.
如图,在平面直角坐标系中,点M的坐标是(5,4),⊙M与y轴相切于点C,与x轴相交于A,B两点. 如图,在△ABC中,AB=AC,∠A=40°,点D在AC上,BD=BC,求∠ABD的度数.
如图,在△ABC中,AB=AC,∠A=40°,点D在AC上,BD=BC,求∠ABD的度数.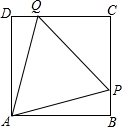 如图,在边长为10的正方形ABCD中,△PAQ是正三角形,求PB的长.
如图,在边长为10的正方形ABCD中,△PAQ是正三角形,求PB的长.