题目内容
5.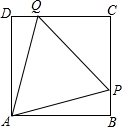 如图,在边长为10的正方形ABCD中,△PAQ是正三角形,求PB的长.
如图,在边长为10的正方形ABCD中,△PAQ是正三角形,求PB的长.
分析 设PB=x,根据正方形以及等边三角形的性质求出PQ与PC的表达式,然后利用勾股定理列出方程求出x的值.
解答 解:设PB=x,
∴PC=10-x,
由题意可知:AD=AB,AQ=AP
在Rt△AQD与Rt△APB中,
$\left\{\begin{array}{l}{AQ=AP}\\{AD=AB}\end{array}\right.$
∴Rt△AQD≌Rt△APB(HL)
∴DQ=PB=x,
∴CQ=10-x,
在Rt△APB中,AP2=100+x2,
在Rt△CQP中,AP2=CQ2+PC2,
∴100+x2=2(10-x)2
化简:x2-40x+100=0,
解得:x=20±10$\sqrt{3}$,
∵x<10,
∴PB=x=20-10$\sqrt{3}$
点评 本题考查正方形以及等边三角形的性质,涉及勾股定理,全等三角形的判定与性质,一元二次方程的解法.

练习册系列答案
相关题目
15. 如图是一个五角星图案,则∠A+∠B+∠C+∠D+∠E的度数是( )
如图是一个五角星图案,则∠A+∠B+∠C+∠D+∠E的度数是( )
 如图是一个五角星图案,则∠A+∠B+∠C+∠D+∠E的度数是( )
如图是一个五角星图案,则∠A+∠B+∠C+∠D+∠E的度数是( )| A. | 180° | B. | 150° | C. | 135° | D. | 120° |
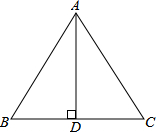 在等腰△ABC中,AB=AC=10cm,BC=12cm,求BC边上的高AD及△ABC的面积.
在等腰△ABC中,AB=AC=10cm,BC=12cm,求BC边上的高AD及△ABC的面积.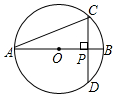 如图,AB是⊙O的直径,弦CD⊥AB,垂足为点P,若AB=4,AC=2$\sqrt{3}$,
如图,AB是⊙O的直径,弦CD⊥AB,垂足为点P,若AB=4,AC=2$\sqrt{3}$, 在2016年宝应以“不忘初心,继续前进”为主题的青年千人毅行中,随机抽得12名选手所用的时间(单位:分钟)得到如下样本数据:
在2016年宝应以“不忘初心,继续前进”为主题的青年千人毅行中,随机抽得12名选手所用的时间(单位:分钟)得到如下样本数据: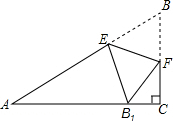 如图,在△ABC中,∠C=90°,点E,F分别在边AB,BC上,沿直线EF将△EBF翻折,使顶点B的对应点B1落在AC边上,且EB1⊥AC.求证:四边形BFB1E是菱形.
如图,在△ABC中,∠C=90°,点E,F分别在边AB,BC上,沿直线EF将△EBF翻折,使顶点B的对应点B1落在AC边上,且EB1⊥AC.求证:四边形BFB1E是菱形.