题目内容
3.如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论正确的是( )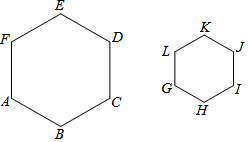
| A. | ∠B=2∠K | |
| B. | 六边形ABCDEF的周长=六边形GHIJKL的周长 | |
| C. | BC=2HI | |
| D. | S六边形ABCDEF=2S六边形GHIJKL |
分析 根据相似多边形的性质对各选项进行逐一分析即可.
解答 解:A、∵六边形ABCDEF∽六边形GHIJKL,∴∠E=∠K,故本选项错误;
B、∵六边形ABCDEF∽六边形GHIJKL,相似比为2:1,∴六边形ABCDEF的周长=六边形GHIJKL的周长×2,故本选项错误;
C、∵六边形ABCDEF∽六边形GHIJKL,相似比为2:1,∴BC=2HI,故本选项正确;
D、∵六边形ABCDEF∽六边形GHIJKL,相似比为2:1,∴S六边形ABCDEF=4S六边形GHIJKL,故本选项错误.
故选C.
点评 本题考查的是相似多边形的性质,即两个相似多边形的对应角相等,周长的比等于相似比,面积的比等于相似比的平方.

练习册系列答案
相关题目
11. (1)如图,木棒AB位于点光源P和地面CD之间,AB∥CD,若光源P到木棒AB的距离是1米,木棒AB到底面的距离也为1米,测得木棒AB的长度为2米,求木棒AB在地面的影长CD;
(1)如图,木棒AB位于点光源P和地面CD之间,AB∥CD,若光源P到木棒AB的距离是1米,木棒AB到底面的距离也为1米,测得木棒AB的长度为2米,求木棒AB在地面的影长CD;
(2)若木棒AB=2米,木棒AB始终保持与地面CD平行,且木棒AB到底面的距离也为1米,类.比(1)的探究方法,填写如表:
(3)平行于地面的线段长度一定,其上方的光源到该线段的距离一定,则当线段逐渐远离地面时,该线段在地面上的影长逐渐变大(填“变大”或“变小”).
 (1)如图,木棒AB位于点光源P和地面CD之间,AB∥CD,若光源P到木棒AB的距离是1米,木棒AB到底面的距离也为1米,测得木棒AB的长度为2米,求木棒AB在地面的影长CD;
(1)如图,木棒AB位于点光源P和地面CD之间,AB∥CD,若光源P到木棒AB的距离是1米,木棒AB到底面的距离也为1米,测得木棒AB的长度为2米,求木棒AB在地面的影长CD;(2)若木棒AB=2米,木棒AB始终保持与地面CD平行,且木棒AB到底面的距离也为1米,类.比(1)的探究方法,填写如表:
| 光源P到木棒AB的距离 | 木棒AB在地面的影长 |
| 1米 | 4 |
| 2米 | 3 |
| 3米 | $\frac{8}{3}$ |
| …. | |
| 结论:平行于地面的线段长度一定,到地面的距离一定,则其上方的光源逐渐远离线段时,该线段在地面上的影长逐渐变小(填“变大”或“变小”). | |
18. 如图,在△ABC中,AB=AC,∠A=40°,以C为圆心,CB的长为半径画弧,交AB于点D,连接CD,则∠ACD等于( )
如图,在△ABC中,AB=AC,∠A=40°,以C为圆心,CB的长为半径画弧,交AB于点D,连接CD,则∠ACD等于( )
 如图,在△ABC中,AB=AC,∠A=40°,以C为圆心,CB的长为半径画弧,交AB于点D,连接CD,则∠ACD等于( )
如图,在△ABC中,AB=AC,∠A=40°,以C为圆心,CB的长为半径画弧,交AB于点D,连接CD,则∠ACD等于( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
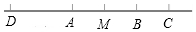 已知线段AB=20cm,点M是线段AB的中点,点C是AB延长线上一点,AC=3BC,点D是线段BA延长线上一点,AD=AB.
已知线段AB=20cm,点M是线段AB的中点,点C是AB延长线上一点,AC=3BC,点D是线段BA延长线上一点,AD=AB.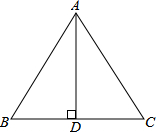 在等腰△ABC中,AB=AC=10cm,BC=12cm,求BC边上的高AD及△ABC的面积.
在等腰△ABC中,AB=AC=10cm,BC=12cm,求BC边上的高AD及△ABC的面积. 如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.
如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.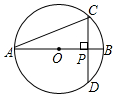 如图,AB是⊙O的直径,弦CD⊥AB,垂足为点P,若AB=4,AC=2$\sqrt{3}$,
如图,AB是⊙O的直径,弦CD⊥AB,垂足为点P,若AB=4,AC=2$\sqrt{3}$,