题目内容
18.已知x=$\sqrt{3}-2$,求代数式x4+4x3-3x2-4x-4的值.分析 由于x=$\sqrt{3}-2$,则x+2=$\sqrt{3}$.所以可将原式尽量化为含有(x+2)2或x+2的代数式,再代入x+2的值,依次计算,最后化简即可.
解答 解:由x=$\sqrt{3}-2$可得x+2=$\sqrt{3}$
原式=x4+4x3+4x2-7x2-4x-4
=x2(x2+4x+4)-7x2-4x-4
=x2(x+2)2-7x2-4x-4
=3x2-7x2-4x-4
=-4x2-4x-4
=-4x2-8x+4x-4
=-4x(x+2)+4x+8-12
=-4x(x+2)+4(x+2)-12
=4(x+2)(1-x)-12
=4$\sqrt{3}$×[1-($\sqrt{3}$-2)]-12
=4$\sqrt{3}$×(3-$\sqrt{3}$)-12
=12$\sqrt{3}$-12-12
=12$\sqrt{3}$-24
点评 本题考查了二次根式的化简求值,以及分解因式的应用,正确对所求的式子进行变形是关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
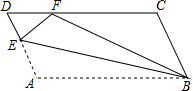 如图,平行四边形ABCD中,点E在AD上,以BE为折痕,把△ABE向上翻折,点A正好落在CD边的点F处.若△FDE的周长为6,平行四边形ABCD的周长为26,那么CF的长为7.
如图,平行四边形ABCD中,点E在AD上,以BE为折痕,把△ABE向上翻折,点A正好落在CD边的点F处.若△FDE的周长为6,平行四边形ABCD的周长为26,那么CF的长为7. 如图,已知AB∥CD,直线MN分别交AB,CD于点M,N,NG平分∠MND,若∠1=70°,求∠2的度数.
如图,已知AB∥CD,直线MN分别交AB,CD于点M,N,NG平分∠MND,若∠1=70°,求∠2的度数.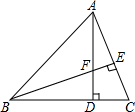 如图,AD,BE为△ABC的高,交点为F,且有BF=AC,FD=CD,证明:BD=AD.
如图,AD,BE为△ABC的高,交点为F,且有BF=AC,FD=CD,证明:BD=AD. 小球在如图所示的地板上自由地滚动,并随机地停留在某块方砖上,那么小球最终停留在黑色区域的概率是$\frac{2}{9}$.
小球在如图所示的地板上自由地滚动,并随机地停留在某块方砖上,那么小球最终停留在黑色区域的概率是$\frac{2}{9}$.