Question

4．如图1，矩形ABCD中，AB=7cm，AD=4cm，点E为AD上一定点，F为AD延长线上一点，且DF=acm，点P从A点出发，沿AB边向点B以2cm/s的速度运动，运动到B点停止，连结PE，设点P运动的时间为ts，△PAE的面积为ycm²，当0≤t≤1时，△PAE的面积y（cm²）关于时间t（s）的函数图象如图2所示，连结PF，交CD于点H．
（1）t的取值范围为0≤t≤3.5，AE=1cm；
（2）如图3，将△HDF沿线段DF进行翻折，与CD的延长线交于点M，连结AM，当a为何值时，四边形PAMH为菱形？
（3）在（2）的条件下求出点P的运动时间t．

Answer 1

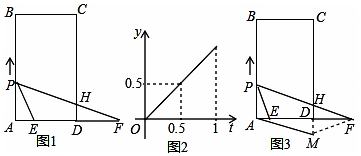
分析 （1）根据AB的长以及点P的移动速度，可以确定t的范围；根据题意可知，y=$\frac{1}{2}$×2t×AE，由图2可知，当t=0.5时，y=0.5，进而得出0.5=$\frac{1}{2}$×2×0.5×AE，即可求出AE．
（2）根据菱形的性质以及轴对称的性质，即可证明∠MAD=∠MFD=30°，最后根据等腰三角形的性质，即可解决问题．
（3）令PA=x，则PF=2x，根据勾股定理可得，PF²=PA²+AF²，即可得出方程（2x）²=x²+8²，求得x的值即可得到点P的运动时间t．

解答 解：（1）∵AB=7，而7÷2=3.5，
∴0≤t≤3.5，
由题意可知，y=$\frac{1}{2}$×2t×AE，
由图2可知，当t=0.5时，y=0.5，
∴0.5=$\frac{1}{2}$×2×0.5×AE，
∴AE=1，
故答案分别为：0≤t≤3.5，1；

（2）如图3，∵四边形AMHP是菱形，
∴AM=MH=2DM，AM∥PF，
∵∠ADM=90°，DM=$\frac{1}{2}$AM，
∴∠MAD=30°，
∴∠PFA=MFA=∠MAD=30°，
∴MA=MF，
∵MD⊥AF，
∴AD=DF=4，
∴a=4．

（3）当a=4cm时，FA=AD+DF=8cm，
令PA=x，则PF=2x，
根据勾股定理可得，PF²=PA²+AF²，
即（2x）²=x²+8²，
解得x=$\frac{{8\sqrt{3}}}{3}$，（负值已舍去）
∴P的运动时间为$\frac{{8\sqrt{3}}}{3}$÷2=$\frac{4}{3}\sqrt{3}$秒．

点评 本题属于四边形综合题，主要考查了矩形的性质，菱形的性质，一次函数的应用以及勾股定理的运用，解题的关键是掌握：菱形的对角线互相垂直平分．解题时注意方程思想的运用．