题目内容
13.为了对中小学进行传统文化教育,上级主管部门开展了“送戏下乡”活动,某九年一贯制学校为了了解本校1600名学生对“送戏下乡”的关注程度,以便做好引导和教育工作,随机抽取了200名学生进行调查,按年级人数和关注程度,分别绘制了条形统计图(图1)和扇形统计图(图2).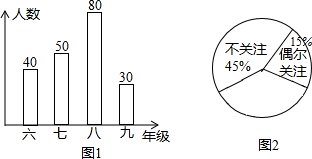
(1)如果把“特别关注”、“一般关注”、“偶尔关注”都统计成关注,那么全校关注本次“送戏下乡”的学生大约有多少名?
(2)在这次调查中,四年级共有甲、乙、丙、丁四人“特别关注”本次“送戏下乡”,现准备从四人中随机抽取两人进行座谈,请用列表法或画树状图的方法求出抽取的两人恰好是甲和乙的概率.
分析 (1)根据扇形统计图找出关注“送戏下乡”活动的百分比,乘以1600即可得到结果;
(2)画树状图得出所有等可能的情况数,找出恰好是甲与乙的情况,即可确定出所求概率.
解答 解:(1)1600×(1-45%)=880(人).
∴该校关注本次“送戏下乡”的学生大约有880人.
(2)画树状图,如图所示:
由图可知,共有12种等可能结果,其中恰好是甲和乙的有2种结果.
∴P(恰好是甲和乙)=$\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查的是条形统计图和扇形统计图以及求随机事件的概率问题的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
 如图,A、B两点在反比例函数y=$\frac{k}{x}$(x>0)的图象上,其中k>0,AC⊥y轴于点C,BD⊥x轴于点D,且AC=1
如图,A、B两点在反比例函数y=$\frac{k}{x}$(x>0)的图象上,其中k>0,AC⊥y轴于点C,BD⊥x轴于点D,且AC=1 已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点,直线AB与y轴交于点C.
已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点,直线AB与y轴交于点C.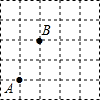 在如图的方格纸中,每个小方格都是边长为1的正方形,点A、B是方格中的两个格点(即网格中横、纵线的交点),在这个5×5的方格纸中,格点C使△ABC的面积为2个平方单位,则图中这样的点C有( )个.
在如图的方格纸中,每个小方格都是边长为1的正方形,点A、B是方格中的两个格点(即网格中横、纵线的交点),在这个5×5的方格纸中,格点C使△ABC的面积为2个平方单位,则图中这样的点C有( )个.